われわれは、サンプルを取ってサンプルのデータを解析することがあります。
このとき、われわれが知りたいのは、サンプルの平均値や標準偏差などの統計量ではなく、姿の見えない母集団の母数(母平均、母分散)であることが一般的です。
サンプルの結果をもとに、母平均が特定の値と言えるかどうか、別のグループの母集団と母分散が異なるのかどうかなどを判断したいわけですね。
このようなときに役に立つのが、統計的検定(単に、検定ということが多い)の考え方です。
身近な例では、医薬品の効果があると言えるかを判断するときに、治験の結果をもとに検定の考え方が使われます。
検定にはいくつかの種類があるので、何回かに分けて解説していきます。
1. 検定とは
今回は、母分散の値が既知の場合の母平均の検定を事例として、検定の考え方を紹介します。
現実の世界では母分散の値が既知であることはあり得ないので、この記事で紹介する方法は実務で使われることはめったにありません。
実践的な検定方法は次の記事以降で解説しますので、今回の記事は検定の考え方を知ることが目的と理解してください。
1-1. 基本事項
今回は正規分布の母平均を推測の対象としますので、まずは以下の2つ基本事項を理解してから読み進めてください。
\(x_1, x_2, \cdots ,x_n \)が互いに独立で正規分布\(N(\mu,\sigma^2)\)に従うとき、そこから\(n\)個抜き取って求めた平均\(\bar{x}\)は正規分布\(N(\mu,\sigma^2/n)\)に従う。
【解説】
正規分布\(N(\mu,\sigma^2)\)の母集団から、\(n\)個のサンプルを抜き取って平均\(\bar{x}\)を計算するという作業を何回も繰り返すと、当然\(\bar{x}\)は毎回同じ値ではなくある分布に従ってばらつきます。
\(\bar{x}\)は正規分布に従うことを示しているのが基本事項1です。
母平均は元の母集団と同じ\(\mu\)ですが、分散がサンプル数で異なります。
分散の分母に\(n\)が入っていることからお分かりいただけると思いますが、抜き取るサンプルの数が多いほど、\(\bar{x}\)のばらつきは小さくなります。


とにかく、基本事項1で覚えておきたいことは、正規分布に従う母集団から抽出したサンプルの平均値は正規分布に従う、ということです。
これは中心極限定理というのですが、実は元の母集団は正規分布に限定されておらず、どんな分布でもサンプルの平均値は正規分布に従うという定理なのです。
ここでは中心極限定理の詳細は述べませんので、興味がある方はExcelなどでシミュレーションしてみてください。
\(\bar{x}\)を標準化すると、
$$u=\displaystyle \frac{\bar{x}-\mu}{\sqrt{\sigma^2/n}}$$
は標準正規分布\(N(0,1^2)\)に従う。
【解説】
以前の記事で、正規分布の標準化について解説しました。
標準化とは、ある正規分布上のある値が、標準正規分布上のどの位置に相当するかに変換する方法でしたね。
\(N(\mu,\sigma^2)\)上の\(x\)を標準化した\(u\)は以下のように求めました。
$$u=\frac{x-\mu}{\sigma}$$
基本事項1より、\(\bar{x}\)は\(N(\mu,\sigma^2/n)\)に従うので、標準化の式の分母の\(\sigma\)を\(\sqrt {\sigma^2/n}\)に変えると基本事項2が成り立つことが分かります。
1-2. 検定の考え方
基本事項を確認しましたので、以下の事例を使って検定の考え方を詳しく見ていきます。
ある製品について、製品の重量(g)の分布は過去の実績から\(N(6.40,0.45^2)\)であることが分かっていますが、材料メーカーを変更することとなりました。
材料の成分は変わらないことから、重量のばらつき(母分散)はメーカー変更前から変化しないと予測できるものの、重量の母平均は変化する可能性があります。
そこで、メーカーを変えた材料を使って試作を行い、9個のサンプルを採取して母平均が変化したか調査することとしました。
サンプル9個の重量を測定したところ、平均\(\bar{x}\)は\(\bar{x}=6.80\)でした。
変更前の重量の母平均=6.40と比べて、変更後の母平均は変化したと言えるでしょうか。
【解説】
\(\bar{x}=6.80\)はあくまでサンプル9個の平均値であり、母平均ではありません。
したがって、\(\bar{x}\neq 6.40\)だからといって、すぐに\(\mu \neq 6.40\)と判断できません。
そこで重要となるのが、母平均\(\mu =6.40\)の母集団から9個サンプリングして平均を求めたとき、\(\bar{x}=6.80\)がどれだけ自然に起こり得るか、つまり、どの程度の発生確率なのか、です。
さて、前項の基本事項1で見たように、正規分布\(N(\mu,\sigma^2)\)に従う母集団から\(n\)個をサンプリングして求めた平均\(\bar{x}\)は、正規分布\(N(\mu,\sigma^2/n)\)に従うのでしたね。
もし、重量の母平均が変化していないのであれば、\(\bar{x}\)は正規分布\(N(6.40,0.450^2/9)\)に従うはずです。
そこで、\(\bar{x}=6.80\)は正規分布\(N(6.40,0.450^2/9)\)から発生すると考えて自然かどうかが判断の拠り所となります。
自然かどうかを判断するには確率を考えます。
つまり、正規分布\(N(6.40,0.450^2/9)\)で6.80以上が出現する確率を求めればよいのです。
確率の求め方はここで解説した通り、Excelまたは数値表を使って求められ、その確率は0.0038(0.38%)となります。
なお、数値表を使って確率を求める場合は、以下のように標準化して正規分布表から確率を求めます。
$$u=\frac{6.80-6.40}{\sqrt{0.450^2/9}}=2.67$$
確率が0.38%ということは、このようなデータを1000回取ったとき、わずか4回程度しか発生する可能性がないということです。
発生確率がこれだけ小さいと、重量の母平均は変化していないものの、たまたまめったに生じないようなデータが得られたというより、そもそも重量の母平均が変化したと考えたくなりますね。
さて、0.38%という確率は非常に小さな確率ですが、どのくらい確率が小さければめったに生じない現象と判断するかの判断基準をあらかじめ決めておく必要があります。
その確率を\(\alpha\)とすると、サンプルデータから計算した確率が\(\alpha\)以下のとき、重量の母平均は変化したと判断します。
このように、母集団に対する前提条件(仮説)を設定して、その真偽をデータから統計的に判定する手順を統計的検定(または単に、検定)と言います。
検定において、あらかじめ設定した確率\(\alpha\)を有意水準または危険率と呼び、通常は\(\alpha=0.05~(5\%)\)に設定します。
事例の場合は\(\bar{x}\)が6.80以上となる確率は0.0038で\(\alpha=0.05\)より小さいので、重量の母平均は変化したと判断できます。
1-3. 帰無仮説と対立仮説
検定を行うときは、まず仮説を設定する必要があります。
先ほどの事例は、「材料メーカー変更後も重量の母平均は変化せず\(\mu=6.40\)である」が仮説に該当します。
「重量の母平均が変化しない」という仮説は、
\(~~H_0:\mu=6.40\)
のように表し、\(H_0\)のことを帰無仮説と言います。
帰無仮説が正しくないと判断したとき、代わりに採択する仮説が対立仮説\(H_1\)です。
事例では、「メーカー変更後の重量の母平均が変更前の母平均から変化したかどうか」を問題にしていたので、以下の対立仮説を設定します。
\(~~ H_1:\mu \neq6.40\)
このように、検定を行う際はまず、帰無仮説\(H_0\)と対立仮説\(H_1\)を設定します。
1-4. 採択域と棄却域
設定した対立仮説に合わせて、棄却域という領域を設定します。
棄却域とは、有意水準\(\alpha\)より小さい確率で帰無仮説\(H_0\)を棄却する\(u\)の領域のことです。
Excelでダイレクトに確率(\(p\)値と言います)を求める場合は、わざわざ棄却域を求める必要はありませんが、数値表を使って判定したいときは棄却域を求めると便利です。
また、この後の記事で解説する推定を行う際に、棄却域が重要になります。
\(\bar{x}\)を、
\(~~u_0=\displaystyle \frac{\bar{x}-6.40}{\sqrt{0.450^2/9}}\)
と標準化すると、\(u_0\)は帰無仮説\(H_0\)の下で標準正規分布\(N(0,1^2)\)に従います。
もし、メーカー変更後の重量の母平均が6.40より大きければ、\(u_0\)は正の大きな値になり、逆に母平均が6.40より小さければ、\(u_0\)は絶対値の大きい負の値になると推測できます。
そこで、有意水準\(\alpha=0.05\)を二等分し、標準正規分布の上側と下側に2.5%ずつを均等に配分し、2.5%の外側を棄却域(\(H_0\)を棄却する領域)とします。
このとき、棄却域は以下のように表せます。
棄却域:\(|u_0|\ge K_{0.025}=1.96\)
\(K_{0.025}=1.96\)は、数値表かExcelのNORM.S.INV関数で求められます。
Excelのセルに「=NORM.S.INV(0.025)」と入力すると、「-1.96」が得られます。
NORM.S.INV関数は、下側の値を返すので-の符号が付きます。
正規分布は左右対称なので、-符号を外した値が上側の値に該当します。
初めから+の値で得たいのであれば、「=NORM.S.INV(0.975)」と入力してください。
\(K_{0.025}\)は標準正規分布の上側確率が2.5%になる点を表し、この点を棄却限界値と言います。
そして、棄却域でない中央付近の領域\(|u_0|<1.960\)を採択域と言います。
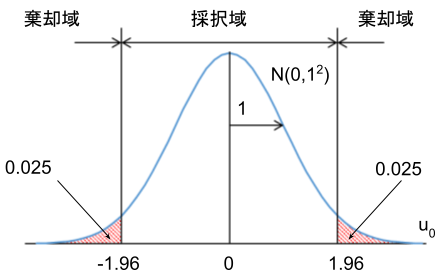
サンプルから計算した\(u_0\)が棄却域に入れば、有意水準5%で有意と判断し、帰無仮説\(H_0\)を棄却して対立仮説を支持します。
事例の場合であれば、メーカー変更後の重量の母平均は6.40と異なる、と判断します。
有意とは、サンプルから求めた\(\bar{x}\)は、帰無仮説\(H_0\)の下では母平均\(\mu=6.40\)と意味のある差がある、という意味です。
\(u_0\)はそれが棄却域に入るか、採択域に入るかで検定結果が決まる重要な統計量なので、検定の世界では検定統計量と呼びます。
ところで、\(u_0\)が採択域に入った場合はどう判断すればよいでしょうか?
採択域に入ったので、対立仮説ではなく帰無仮説を採択する、と安易に判断してはいけません。
この場合は「帰無仮説を棄却できず、メーカー変更後の重量の母平均は6.40と異なるとは言えない」という結論になります。
後ほど解説しますが、検定には2種類の誤りがあり、「帰無仮説を採択する」と断定すると、第2種の誤りの確率が大きくなり得るため、「帰無仮説を棄却できない」という奥歯にものが挟まったような消極的な結論を出さざるを得ないのです。
ただし、実務においては、帰無仮説を棄却できない場合は、帰無仮説が成り立つとみなして、次のプロセスに進むことが多いです。
1-5. 検定方式
先ほど、棄却域を設定する際に、有意水準を2等分して標準正規分布の上側に設定しました。
このように、両側に棄却域を設定する検定方式を両側検定と呼びます。
両側検定以外に、片側検定という検定方式もあります。
事例の場合であれば、メーカー変更後の重量の母平均が変化するなら、6.40より大きくなるはずだとある程度確信を持てるのであれば、対立仮説\(H_1\)を以下のように設定します。
\(~~H_1:\mu>6.40\)
この場合、標準正規分布の下側には棄却域を設定せず、上側のみに5%の確率を集めて棄却域を設定します。
このとき、棄却域は以下のように表せます。
棄却域:\(u_0\ge K_{0.05}=1.645\)
Excel関数で求める場合、セルに「=NORM.S.INV(0.05)」と入力して得られた値のー符号を外した値を採用するか、セルに「=NORM.S.INV(0.95)」と入力して得られた値を採用してください。

棄却域が標準正規分布の上側(右側)のみにあるので、右片側検定と言います。
同じように、重量の母平均が変化するなら、6.40より小さくなるはずだとある程度確信を持てるのであれば、対立仮説\(H_1\)を以下のように設定します。
\(~~H_1:\mu<6.40\)
この場合、標準正規分布の上側には棄却域を設定せず、下側のみに5%の確率を集めて棄却域を設定します。
このとき、棄却域は以下のように表せます。
棄却域:\(u_0 \le -K_{0.05}=-1.645\)
Excel関数で求める場合、セルに「=NORM.S.INV(0.05)」と入力して得られた値を採用してください。

棄却域が標準正規分布の下側(左側)のみにあるので、左片側検定と言います。
なお、片側検定の帰無仮説\(H_0\)の表現は、両側検定と同じです。
母平均が大きくなるか小さくなるか分からない場合は、両側検定を選ぶのが無難です。
ただし、両側検定と片側検定のどちらの検定方式で検定するかは、必ず検定の初めに決定してください。(計算結果を見てから、検定方式を選ばないこと。)
1-6. 検定における2種類の誤り
検定は少ないデータで母集団を姿を判断するので、当然のことながら判断を誤る可能性があります。
検定においては、2種類の誤りが存在します。
本当は帰無仮説\(H_0\)が成立しているにもかかわらず、\(H_0\)を棄却してしまう誤りを第1種の誤りといい、この誤りを犯す確率は有意水準\(\alpha\)と同じです。
第1種の誤りは、「あわてものの誤り」とも言います。
母平均が従来と変わっていないにも関わらず、変わったと慌てて判断してアクションを取ってしまう誤りです。
一方、帰無仮説\(H_0\)が成立していないにもかかわらず、\(H_0\)を棄却しない誤りを第2種の誤りといい、この誤りを犯す確率を\(\beta\)で表します。
第2種の誤りは、「ぼんやりものの誤り」とも言います。
母平均が従来と変わったにも関わらず、変わっていないとぼんやり判断してアクションを取らない誤りです。
対立仮説が成立しているときに、それを正しく検出する確率、つまり、帰無仮説を棄却する確率を検出力と言い、\(1-\beta\)で表せます。
検定における2種類の誤りをまとめたものが、以下の表です。
| 本当に成り立っているのは | |||
| \(H_0\) | \(H_1\) | ||
| 検定結果 | \(H_0\) 有意でない | 正しい (確率:\(1-\alpha\)) | 第2種の誤り (確率:\(\beta\)) |
| \(H_1\) 有意である | 第1種の誤り (確率:\(\alpha\)) | 正しい (確率:\(1-\beta=\)検出力) | |
2. 検定の流れ
母分散が既知の場合の、母平均の検定手順を解説します。
この手順は、その他の検定の場合でも適用できるので、ここで検定の進め方をマスターしておいてください。
手順1. 帰無仮説\(H_0\)と対立仮説\(H_1\)を設定する。
検定の目的に応じて、(1)~(3)のいずれかを選択します。
(1) \(H_0:\mu=\mu_0\) (\(\mu_0\)は指定された値)
\(H_1:\mu \neq \mu_0\) (両側検定)
(2) \(H_0:\mu=\mu_0\) (\(\mu_0\)は指定された値)
\(H_1:\mu > \mu_0\) (右片側検定)
(3) \(H_0:\mu=\mu_0\) (\(\mu_0\)は指定された値)
\(H_1:\mu < \mu_0\) (左片側検定)
手順2. 有意水準\(\alpha\)を決める。
通常は、\(\alpha=0.05\)とします。
手順3. 手順1(仮説)と手順2(有意水準)に対応した棄却域を決める。
(1)棄却域:\(|u_0|\ge K_{\alpha/2}\) (\(\alpha=0.05\)なら\(K_{0.025}=1.96\)) (両側検定)
(2)棄却域:\(u_0 \ge K_{\alpha}\) (\(\alpha=0.05\)なら\(K_{0.05}=1.645\)) (右片側検定)
(3)棄却域:\(u_0 \le -K_{\alpha}\) (\(\alpha=0.05\)なら\(K_{0.05}=1.645\)) (左片側検定)
手順4. 採取したデータ\(x_1,x_2.\cdots,x_n\)から、検定統計量\(u_0\)の値を計算する。
$$u_0=\displaystyle \frac{\bar{x}-\mu_0}{\sqrt{\sigma^2/n}}$$
手順5. 判定する。
\(u_0\)が棄却域に入れば、有意水準\(\alpha\)で有意と判定し、帰無仮説\(H_0\)を棄却して対立仮説\(H_1\)を採択します。
\(u_0\)が棄却域に入らなければ、有意水準\(\alpha\)で有意でないと判定し、帰無仮説\(H_0\)を棄却しません。
具体的な事例で、検定手順を確認しましょう。
コストダウンのため、材料の仕入先を変更することになりました。
仕入先変更後の材料を用いたとき、製品の重量の母平均が従来の母平均\(\mu_0=139.0g\)から変化するかどうかを検定したいと考えています。
サンプルを8個採取して重量を測定し、以下の測定結果を得ました。(単位:g)
149, 152, 135, 147, 150, 141, 140, 138
仕入先変更材料を使ったとき、重量の母平均が異なると言えるかどうかを検定で判断しましょう。
ただし、母分散は従来の\(\sigma^2=6.0^2\)と変わらないものとします。
【解説】
検定の手順にしたがって、検定を進めます。
手順1
帰無仮説\(H_0:\mu=139.0\)
対立仮説\(H_1:\mu \neq 139.0\)
母平均が異なるかどうか(大きいか小さいかは、分からない)を検定するので、今回は両側検定で検定します。
手順2
\(\alpha=0.05\)
手順3
棄却域:\(|u_0|\ge K_{0.025}=1.96\)
手順4
データの平均\(\bar{x}=144.0\)、データの個数\(n=8\)、母分散\(\sigma^2=6.0^2\)であることから、検定統計量\(u_0\)は以下のように求まります。
$$u_0=\displaystyle \frac{\bar{x}-\mu_0}{\sqrt{\sigma^2/n}}=\frac{144.0-139.0}{\sqrt{6.0^2/8}}=2.357$$
手順5
\(|u_0|=2.357 \ge K_{0.025}=1.96\)なので、5%有意です
よって、帰無仮説\(H_0\)を棄却し、「仕入先変更品を使った場合の母平均は、従来の母平均\(\mu_=139.0\)と異なる」と判断します。
3. 実践のためのアドバイス
着目する特性値に差があるかどうかを統計的に判断するのが、検定です。
検定をマスターすれば、第三者に対する説得力を増せたり、ある対策が効果があったかどうかを数値で判断できたりできるといったメリットがあります。
理解するためのハードルは高いですが、本サイトではさまざまな検定方法を丁寧に解説していきますので、ご安心ください。
4. おわりに
今回は、検定の考え方と進め方を解説しました。
独特の用語がたくさん出てくるので、統計の初学者にとって検定は大きなハードルとなる内容です。
他にも、いろいろな種類の検定がありますが、基本的な考え方はすべて同じなので、この記事で検定の考え方と進め方をしっかりマスターしてください。






