以前、検定の解説をしました。
 母集団に関する仮説を統計的に検証する~検定の基礎
母集団に関する仮説を統計的に検証する~検定の基礎
今回解説する推定は、検定とセットで解説されることが多いですが、これは検定で帰無仮説が棄却された場合、母数の推定値がいくつなのかを知りたい場面が多いからです。
今回の記事では、母集団の母数を推定する2種類の方法を解説します。
1. 推定とは
検定では、帰無仮説と対立仮説という2つの仮説を設定して、帰無仮説を棄却するかどうかという判断をしました。
これに対して、母平均または母分散がどれくらいになっているかを、具体的な数値で表そうという手法が推定です。
推定には、点推定と区間推定の2種類があるので、それぞれを解説します。
2. 点推定
点推定とは、統計量の値を用いて母数を一つの値で推定する方法のことです。
ここでは、正規分布\(N(\mu,\sigma^2)\)に従う母集団から採取した、\(n\)個のデータ\(x_1, x_2,\cdots,x_n\)を使って母平均\(\mu\)と母分散\(\sigma^2\)を点推定することを考えます。
2-1. 母平均\(\mu\)の点推定
母平均\(\mu\)の点推定は、「母平均は〇〇だろう」の〇〇を求めることです。
〇〇の式で表したものを推定量と呼びます。
母平均\(\mu\)の推定量であることを明確にするために、\(\hat{\mu}=\)〇〇と表すこととします。
データから実際に求めた推定量を、点推定値と呼びます。
普通に考えれば、データから求めた平均\(\bar{x}\)を、母平均の点推定値として採用すればよいはずです。
点推定値はそれで正解なのですが、理論的になぜそう言えるのかを詳しく見ておきます。
以前の記事で解説した、以下の基本事項1を利用します。
\(~~E(\bar{x})=\mu \quad (1)\)
\(~~V(\bar{x})=\displaystyle \frac{\sigma^2}{n} \quad (2)\)
ただし、\(E\)は期待値で、括弧内の確率変数が平均的にどのような値を取るかを表します。
(1)式は、正規分布\(N(\mu,\sigma^2)\)に従う\(n\)個のデータ\(x_1,x_2.\cdots,x_n\)から平均\(\bar{x}\)を計算する作業を例えば100回行うと、100個の\(\bar{x}\)の平均が母平均\(\mu\)にほぼ等しいことを意味します。
(無限回行うと、ちょうど母平均\(\mu\)と等しくなります。)
候補となる推定量の期待値が母数に一致するとき、この推定量を不偏推定量と言います。
\(\bar{x}\)は\(\mu\)を偏りなく推定しているという意味です。
しかし、これだけでは\(\bar{x}\)が\(\mu\)のよい推定量である、と言うには不十分です。
例えば、以下のような3つの値も\(\mu\)の不偏推定量の候補として考えられます。
\(~~\hat{\mu}_1=x_1\)
\(~~\hat{\mu}_2=\displaystyle \frac{x_1+x_2}{2}\)
\(~~\hat{\mu}_3=\displaystyle \frac{x_1+x_2+x_3}{3}\)
これらは、n個のサンプルのうち、1~3個のサンプルを使って点推定値を求めた場合ですが、これらの推定量の期待値も(1)式と同じく、\(E(\hat{\mu}_1)=E(\hat{\mu}_2)=E(\hat{\mu}_3)=\mu\)となります。
したがって、\(\hat{\mu}_1\)、\(\hat{\mu}_2\)、\(\hat{\mu}_3\)はすべて不偏推定量です。
このように、不偏推定量の候補が複数ある場合、どの不偏推定量が最良でしょうか?
ところで不偏推定量とは言っても、平均的に母平均\(\mu\)と等しくなるというだけで、毎回の推定量の値は母平均と一致せずにばらつきます。
したがって、最良の不偏推定量は、母平均\(\mu\)のなるべく近くでばらついている推定量、つまり、分散が最も小さい推定量と言えます。
(2)式より、\(n\)個のデータの平均\(\bar{x}\)の分散は\(V(\bar{x})=\sigma^2/n\)であるのに対して、1~3個のサンプルから求めた推定量の分散は、
\(~~V(\hat{\mu}_1)=\sigma^2\)
\(~~V(\hat{\mu}_2)=\displaystyle \frac{\sigma^2}{2}\)
\(~~V(\hat{\mu}_3)=\displaystyle \frac{\sigma^2}{3}\)
であり、これらはすべて\(\sigma^2/n\)より大きな値を取ります。
よって、\(\bar{x}\)は不偏かつ、分散が最も小さいので、母平均\(\mu\)の最もよい推定量と言えます。
2-2. 母分散\(\sigma^2\)の点推定
母分散\(\sigma^2\)が未知の場合、\(\sigma^2\)の不偏推定量は、平方和\(S=\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})^2\)を\(n-1\)で割った\(V=\displaystyle \frac{S}{n-1}\)です。
つまり、\(E(V)=\sigma^2\)が成り立ちます。
なぜ、平方和\(S\)を\(n\)ではなく\(n-1\)で割るかですが、仮に平方和\(S\)を\(n\)で割った値を\(\sigma^2\)の推定量とするとその期待値は、
\(~~E \left(\displaystyle \frac{S}{n} \right)=\displaystyle \frac{n-1}{n}E\left(\frac{S}{n-1}\right)\)
\(~~~~=\displaystyle \frac{n-1}{n}E(V)\)
\(~~~~=\displaystyle \frac{n-1}{n}\sigma^2<~\sigma^2\)
となり不偏となりません(小さくなります)。
よって、平方和\(S\)を\(n-1\)で割った値を母分散\(\sigma^2\)の点推定値とします。
3. 区間推定
区間推定とは、「母平均は区間(〇〇,△△)の中にあるだろう」と、〇〇と△△を求めて区間で推定することです。
〇〇と△△に挟まれる区間を信頼区間と言い、〇〇を下側信頼限界または信頼下限、△△を上側信頼限界または信頼上限と言います。
母分散の区間推定の方法は、別の記事で紹介するので、今回は母分散が既知の場合の母平均を区間推定してみます。
基本事項1より、正規分布\(N(\mu,\sigma^2)\)から\(n\)個のデータ\(x_1, x2,\cdots,x_n\)をサンプリングするとき、データの平均\(\bar{x}\)は\(N(\mu,\sigma^2/n)\)に従います。
基本事項2より、\(\bar{x}\)を標準化した\(u=\displaystyle \frac{\bar{x}-\mu}{\sqrt{\sigma^2/n}}\)は、標準正規分布\(N(0,1^2)\)に従います。
ここで、標準正規分布において確率\(\alpha\)を両側に\(\alpha/2\)ずつ配分した状況を図示します。
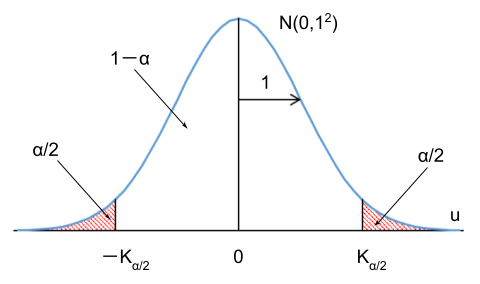
この状況を式で表すと、以下のようになります。
\(~~Pr(-K_{\alpha/2}<u<K_{\alpha/2})=1-\alpha\)
この式に\(u=\displaystyle \frac{\bar{x}-\mu}{\sqrt{\sigma^2/n}}\)を代入して変形すると、以下の式が得られます。
\(~~Pr \left (-K_{\alpha/2}<\displaystyle \frac{\bar{x}-\mu}{\sqrt{\sigma^2/n}}<K_{\alpha/2} \right )\)
\(~~=Pr \left ( \bar{x}-K_{\alpha/2}\sqrt{\displaystyle \frac{\sigma^2}{n}}<\mu<\bar{x}+K_{\alpha/2}\sqrt{\displaystyle \frac{\sigma^2}{n}} \right )=1-\alpha \qquad (3)\)
(3)式は、区間\(\left( \bar{x}-K_{\alpha/2}\sqrt{\displaystyle \frac{\sigma^2}{n}},\bar{x}+K_{\alpha/2}\sqrt{\displaystyle \frac{\sigma^2}{n}} \right )\)に\(1-\alpha\)の確率で母平均\(\mu\)が含まれることを意味します。
このとき、確率\(1-\alpha\)を信頼率と言い、0.95(95%)がよく使われます。
信頼率95%とは、正規分布\(N(\mu,\sigma^2)\)に従う\(n\)個のデータ\(x_1,x_2.\cdots,x_n\)から信頼率95%の信頼区間\(\left( \bar{x}-1.96\sqrt{\displaystyle \frac{\sigma^2}{n}},\bar{x}+1.96\sqrt{\displaystyle \frac{\sigma^2}{n}} \right )\)を求める作業を100回行ったとすると、得られた100個の信頼区間のうち約95個は、母平均\(\mu\)を含むということを意味します。
信頼区間の式を見ると分かりますが、信頼区間の幅はサンプルの数が多く、ばらつきが小さいほど狭くなります。
ここで、母分散が既知の場合の母平均の検定における採択域と、今回の信頼区間は同じではないかと気づいた方がいると思いますが、それは間違っていません。
「有意水準5%の両側検定で、有意にならずに帰無仮説が棄却されないこと」と「帰無仮説の値\(\mu_0\)が信頼率95%の信頼区間に含まれること」は同じこと言っているのです。
4. 推定の例
以前の記事の事例について、検定では有意\((\mu \neq 139.0)\)という結論に至りました。
では母平均はいくつになると推定できるでしょうか。
点推定と区間推定(信頼率95%)を行ってみましょう。
【データ】
149, 152, 135, 147, 150, 141, 140, 138
ただし、母分散は\(\sigma^2=6.0^2\)とします。
1) 点推定
\(\hat{\mu}=\bar{x}=144.0\)
2) 区間推定
信頼率95%の区間推定の式に、データから求めた数値を代入します。
\(~~\left( \bar{x}-K_{0.025}\sqrt{\displaystyle \frac{\sigma^2}{n}},\bar{x}+K_{0.025}\sqrt{\displaystyle \frac{\sigma^2}{n}} \right )\)
\(~~=\left(144.0-1.96\sqrt{\displaystyle \frac{6.0^2}{8}},144.0+1.96\sqrt{\displaystyle \frac{6.0^2}{8}} \right )\)
\(~~=(139.8,~148.2)\)
有意水準5%で帰無仮説が棄却されているので、当然、信頼率95%の信頼区間に139.0は含まれることはありません。
5. 実践のためのアドバイス
サンプルから母集団の母数を推定することは、データ解析の主な目的の一つであり、今回の推定の考え方は母集団を推定する上で必須の考え方です。
単純にサンプルから求めた点推定では、本来の母数と大きく異なることは否めないため、区間推定による推定も非常に大切なので、点推定と区間推定はセットで覚えておきましょう。
6. おわりに
今回は、点推定と区間推定の考え方を解説しました。
サンプルから母集団の姿を知る際に、推定の考え方はとても有効です。
また、検定を行って帰無仮説を棄却しました、じゃあ母平均はいくつなの?と、検定と推定はセットで使われることが多いので、この後の記事では検定と推定をセットで解説することとします。





