以前の記事で、相関係数について解説しました。
 2変数の関係を定量化する方法~相関分析①~
2変数の関係を定量化する方法~相関分析①~
相関係数とは、2つのデータの関係の強さを数値で表す指標でしたね。
算出した相関係数は、あくまで母集団の一部であるサンプルから算出した相関係数であり、母集団の相関については判断できません。
これまでの記事で、母平均と母分散などについて検定や推定できることを述べてきましたが、母集団の相関係数である母相関係数についても検定や推定を適用できます。
今回は、母相関係数に関する検定と推定について解説します。
1. 2次元正規分布について
2つの変数\(x\)と\(y\)があるとしましょう。
おのおのが正規分布に従い、かつ\(x\)と\(y\)の間に相関があるとき、2つの変数\((x, y)\)は2次元正規分布に従います。
\(x\)が1次元正規分布\(N(\mu_x,\sigma_x^2)\)に、\(y\)が\(N(\mu_y,\sigma_y^2)\)に従い、\(x\)と\(y\)の母集団相関係数(母相関係数)が\(\rho\)のとき、2次元正規分布の確率密度関数は、以下の式で与えられます。
\(f(x,y)=\displaystyle \frac{1}{2\pi \sqrt{1-\rho^2}\sigma_x\sigma_y}\)
\(\times \exp \left [ – \displaystyle \frac{1}{2(1-\rho^2)} \left \{ \frac{(x-\mu_x)^2}{\sigma_x^2}-2\rho \frac{(x-\mu_x)(y-\mu_y)}{\sigma_x \sigma_y}+\frac{(y-\mu_y)^2}{\sigma_y^2}\right \} \right ]\)
簡単にするために、\(x\)と\(y\)はともに標準正規分布に従うとすると、\(\mu_x=\mu_x=0, \sigma_x=\sigma_x=1\)なので上の式を簡単にできます。
このとき、\(x\)と\(y\)の母相関係数が\(\rho=0\)(無相関)の場合と、\(\rho=0.9\)(強い正の相関)の場合で、2次元正規分布の形状を比較してみましょう。
| 相関係数 | 角度0 | 90°回転 |
|---|---|---|
| \(\rho=0\) | 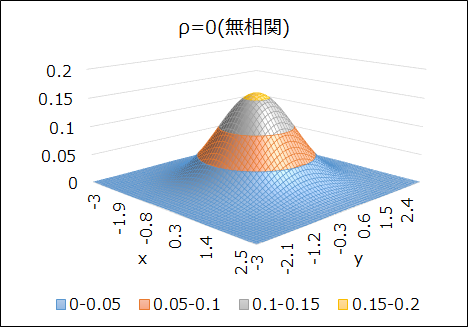 | 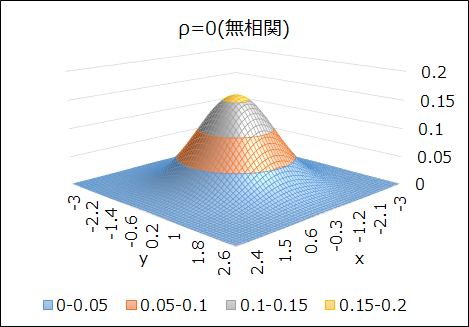 |
| \(\rho=0.9\) | 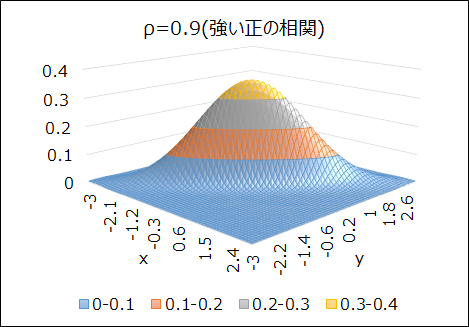 | 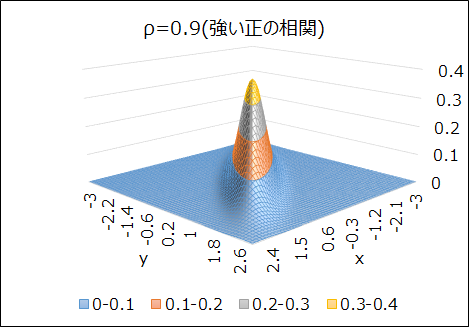 |
\(\rho=0\)のときは90°回転させても分布の形状は変わりませんが、\(\rho=0.9\)になると、相関の影響で細長い形状の分布になっていることが分かります。
散布図は、2次元正規分布からサンプリングしたサンプルを\(x-y\)平面にプロットしたもので、母相関係数\(\rho\)の推定量が標本相関係数\(r\)です。
2. 無相関の検定
対になった2つのデータ\(x,y\)が与えられているとき、\(x\)と\(y\)の関係を分析することを相関分析と言いましたね。
2つの変数の関係の強さを数値で表す指標が、相関係数\(r\)でした。
しかし、われわれが知りたいのは、サンプルの関係の強さではなく、2つの変数の母集団における関係の強さです。
このとき、サンプルから得られた相関係数\(r\)をもとに、母相関係数\(\rho\)について検定で判断することが可能です。
検定する場合、帰無仮説\(H_0\)を\(\rho=0\)とするため、無相関の検定と呼ばれます。
2-1. 無相関の検定手順
手順1. 帰無仮説\(H_0\)と対立仮説\(H_1\)を設定する。
無相関の検定は、通常両側検定で行うので、以下のように設定します。
\(H_0:\rho=0\)
\(H_1:\mu \neq 0\)
手順2. 有意水準\(\alpha\)を決める。
通常は、\(\alpha=0.05\)とします。
手順3. 採取した\(n\)個の2次元データから相関係数\(r\)を求め、検定統計量\(t_0\)の値を計算する。
検定統計量\(t_0\)は、以下のように求めます。
\(t_0=\displaystyle \frac{r \sqrt{n-2}}{\sqrt{1-r^2}}\)
手順4. 検定統計量\(t_0\)の自由度\(\phi\)を求める。
2次元データの個数を\(n\)とすると、自由度\(\phi\)は、
\(\phi=n-2\)
で求められます。
手順5. 棄却域を決める。
棄却域:\(|t_0|\ge t(\phi,\alpha)\)
手順6. 判定する。
\(t_0\)が棄却域に入れば、有意水準\(\alpha\)で有意と判定し、帰無仮説\(H_0\)を棄却して対立仮説\(H_1\)を採択します。
\(t_0\)が棄却域に入らなければ、有意水準\(\alpha\)で有意でないと判定し、帰無仮説\(H_0\)を棄却しません。
2-2. 無相関の検定の実施例
25個の2次元データの相関係数\(r=0.92\)のとき、無相関の検定手順に従って\(\rho \neq 0\)と言えるかどうか、検定してみましょう。
手順1. 帰無仮説\(H_0\)と対立仮説\(H_1\)を設定する。
無相関の検定は、通常両側検定で行うので、以下のように設定します。
\(H_0:\rho=0\)
\(H_1:\mu \neq 0\)
手順2. 有意水準\(\alpha\)を決める。
\(\alpha=0.05\)
手順3. 採取した\(n\)個の2次元データから相関係数\(r\)を求め、以下の検定統計量\(t_0\)の値を計算する。
\(t_0=\displaystyle \frac{0.92 \times \sqrt{25-2}}{\sqrt{1-0.92^2}}=11.26\)
手順4. 検定統計量\(t_0\)の自由度\(\phi\)を求める。
\(\phi=25-2=23\)
手順5. 棄却域を決める。
棄却域:\(|t_0|\ge t(23,0.05)=2.069\)
手順6. 判定する。
\(|t_0|=11.26 \ge t(23,0.05)=2.069\)で検定統計量\(t_0\)は棄却域に入るので有意です。
よって帰無仮説\(H_0\)を棄却して、2つの変数間に相関関係があると判断できます。
3. 母相関係数の推定
以前の記事で解説した通り、母平均\(\mu\)の推定には点推定と区間推定の2種類があります。
母相関係数\(\rho\)を区間推定するにあたり、変換が必要なので具体的な変換方法を見ていきます。
まず、\(n\)個の2次元データの相関係数\(r\)が与えられたとき、
\(z=\displaystyle \frac{1}{2} \ln \left ( \frac{1+r}{1-r}\right )\)
と変換します。(\(z\)変換)
ここで、\(ln\)は自然対数を表します。
このとき、\(z\)は近似的に平均\(\displaystyle \frac{1}{2}ln \left ( \frac{1+\rho}{1-\rho} \right )\)、分散\(\displaystyle \frac{1}{n-3}\)の正規分布に従います。
3-1. 母相関係数の推定手順
点推定はデータの相関係数\(r\)を使えばよいです。
区間推定については、\(z\)が近似的に正規分布に従う性質を利用することで、\(\rho\)の信頼区間を求められます。
\(\displaystyle \frac{exp(2A)-1}{exp(2A)+1} \le \rho \le \displaystyle \frac{exp(2B)-1}{exp(2B)+1}\)
ただし、\(A=z-\displaystyle \frac{K_{\alpha/2}}{\sqrt{n-3}},~B=z+\displaystyle \frac{K_{\alpha/2}}{\sqrt{n-3}}\)です。
また、\(exp(x)=e^x\)で\(e\)は自然対数の底であり、\(K_p\)は標準正規分布における上側\(100p\%\)点です。
4-2. 母相関係数の推定の実施例
無相関の検定で使ったデータ\((n=25, r=0.92)\)で、点推定と区間推定を行ってみましょう。
点推定:
\(\hat{\rho}=r=0.92\)
区間推定:信頼率95%の信頼区間を求めます。
3-1.で求めた各式の値を求めます。
\(z=\displaystyle \frac{1}{2} \ln \left ( \frac{1+0.92}{1-0.92}\right )=1.589\)
\(A=1.589-\displaystyle \frac{1.96}{\sqrt{22}}=1.171\)
\(B=1.589+\displaystyle \frac{1.96}{\sqrt{22}}=2.007\)
\(\displaystyle \frac{exp(2\times 1.171)-1}{exp(2 \times 1.171)+1}=0.825\)
\(\displaystyle \frac{exp(2\times 2.007)-1}{exp(2 \times 2.007)+1}=0.965\)
したがって、母相関係数\(\rho\)の95%信頼区間は、
\(0.825 \le \rho \le 0.965\)
と求められます。
4. おわりに
今回は、母相関係数に関する検定と推定について解説しました。
検定統計量が近似的に正規分布に従うことを利用して、検定や推定が可能です。
2次元データで相関係数を求めたときは、合わせて母相関係数の検定と推定も実施してみてください。







