以前の記事で、母分散が未知の場合の一つの母平均の検定と推定について、基本的な考え方と進め方を解説しました。
 一つの母平均に関する検定と推定(母分散が未知の場合)
一つの母平均に関する検定と推定(母分散が未知の場合)
母平均の検定では、\(t\)分布の性質を使って検定と推定を行いました。
今回は、母分散に注目し、一つの母分散に関する検定と推定について解説します。
1. 適用できる場面
以下の事例を使って、母分散の検定と推定を解説します。
ある薬品の1kg中の有効成分の量は、母分散が\((0.50g)^2\)の正規分布に従っています。最近、最新鋭の新ラインを立ち上げたことから、新ラインで製造した薬品の1kg中の有効成分の母分散が、従来のラインより小さくなったかどうかを検討することになりました。
新ラインからランダムに10個のサンプルを抜き取り、有効成分の量を測定した結果は、以下の通りでした。(単位:g)
10.2, 9.6, 9.9, 10.3, 10.1, 9.8, 10.2, 10.4, 10.1, 10.3
この事例では、新ライン製造品の有効成分の量が正規分布\(N(\mu, \sigma^2)\) (母平均\(\mu\)と母分散\(\sigma^2\)はともに未知)に従うと考えて、この母集団から抜き取られた10個のサンプルのデータに基づいて、一つの母分散\(\sigma^2\)の検定や推定を行うことが目的です。
2. \(\chi^2\)分布について
正規分布に従う母集団からn個のサンプル\(x_1,x_2,\cdots,x_n\)を抽出すると、母分散に関する情報はサンプルの偏差平方和\(S=\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})^2\)やサンプルの分散\(V=\displaystyle \frac{S}{n-1}\)に含まれています。
ここで、以下の基本事項が知られています。
\(n\)個のデータ\(x_1,x_2,\cdots,x_n\)が互いに独立に正規分布\(N(\mu,\sigma^2)\)に従うとき、\(\chi^2=\displaystyle \frac{S}{\sigma^2}\)は自由度\(\phi=n-1\)の\(\chi^2\)分布に従う。
\(\chi^2\)分布という新しい分布が出てきました。
\(Z\)が標準正規分布\(N(0,1^2)\)に従うとき、以下の式で求まる\(\chi^2\)が従う分布を\(\chi^2\)分布と言います。
\(\chi^2=Z_1^2+Z_2^2+\cdots +Z_\phi^2\)
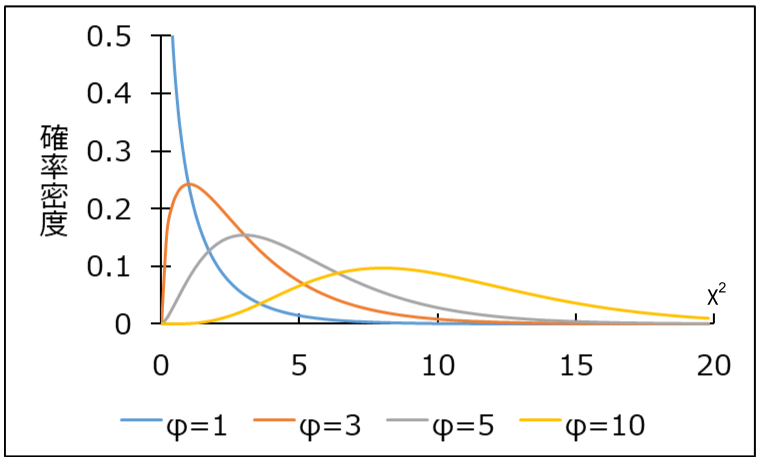
\(\chi^2\)分布は自由度のみによって形状が決まる確率分布で、自由度により形状が異なります。
\(\chi^2\)分布は、これまで出てきた正規分布や\(t\)分布と違って、ゼロ以上の値で定義されていることと、左右非対称の分布形状であることが特徴です。
検定統計量が\(\chi^2\)分布に従うことが分かれば、あとは棄却域を設定して検定統計量が棄却域に入るかどうかを調べることで検定できます。
3. 一つの母分散に関する検定
それでは、母分散の検定手順を見ていきます。
基本的な流れは、以前の記事で解説した母平均の検定の流れと同じですので、異なる点を特に詳しく説明します。
3-1. 一つの母分散の検定手順
手順1. 帰無仮説\(H_0\)と対立仮説\(H_1\)を設定する。
検定の目的に応じて、(1)~(3)のいずれかを選択します。
(1) \(H_0:\sigma^2=\sigma^2_0\) (\(\sigma^2_0\)は指定された値)
\(H_1:\sigma^2 \neq \sigma^2_0\) (両側検定)
(2) \(H_0:\sigma^2=\sigma^2_0\) (\(\sigma^2_0\)は指定された値)
\(H_1:\sigma^2 > \sigma^2_0\) (右片側検定)
(3) \(H_0:\sigma^2=\sigma^2_0\) (\(\sigma^2_0\)は指定された値)
\(H_1:\sigma^2 < \sigma^2_0\) (左片側検定)
手順2. 有意水準\(\alpha\)を決める。
通常は、\(\alpha=0.05\)とします。
手順3. 手順1(仮説)と手順2(有意水準)に対応した棄却域を決める。
(1)棄却域:\(\chi^2_0 \le \chi^2(\phi,1-\alpha/2)\)または\(\chi^2_0 \ge \chi^2(\phi,\alpha/2)\) (両側検定)
(2)棄却域:\(\chi^2_0 \ge \chi^2(\phi,\alpha)\) (右片側検定)
(3)棄却域:\(\chi^2_0 \le \chi^2(\phi,\alpha)\) (左片側検定)
手順4. 採取したデータ\(x_1,x_2.\cdots,x_n\)から、検定統計量\(\chi^2_0\)の値を計算する。
\(~~~\chi^2_0=\displaystyle \frac{S}{\sigma^2_0}\)
\(~~~\phi=n-1\)
手順5. 判定する。
\(\chi^2_0\)が棄却域に入れば、有意水準\(\alpha\)で有意と判定し、帰無仮説\(H_0\)を棄却して対立仮説\(H_1\)を採択します。
\(\chi^2_0\)が棄却域に入らなければ、有意水準\(\alpha\)で有意でないと判定し、帰無仮説\(H_0\)を棄却しません。
3-2. 一つの母分散の検定における棄却域の求め方
母平均の検定では、正規分布または\(t\)分布を使って検定しました。
正規分布と\(t\)分布は左右対称なので、両側検定では左右の棄却限界値の絶対値は同じで、単にーが付くかつかないかの違いでした。
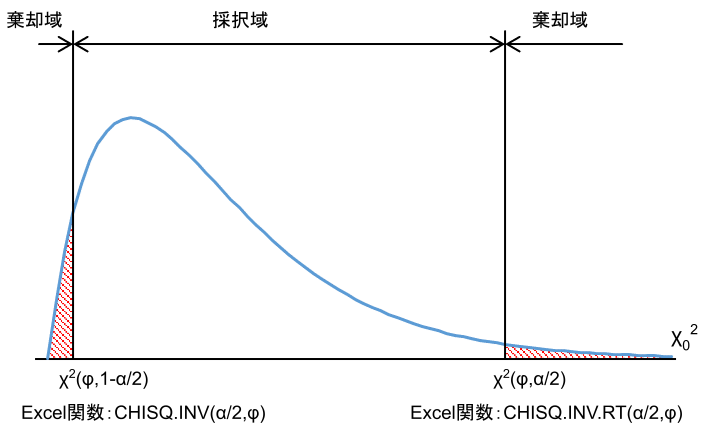
一方、\(\chi^2\)分布は左右非対称のため、両側検定の場合、上側と下側の棄却限界値をそれぞれ求める必要があります。
\(\chi^2\)分布の棄却限界値をExcelで求める場合、以下のようにセルに入力すれば求められます。(有意水準\(\alpha=0.05\)の場合)
【両側検定】
確率5%を上下に2.5%ずつ割り当てます。
下側:「=CHISQ.INV(0.025,\(\phi)\))」と入力して得られる値を採用します。
(\(\phi\)は自由度\(n-1\))
上側:「=CHISQ.INV.RT(0.025,\(\phi)\))」と入力して得られる値を採用します。
【片側検定】
下側:「=CHISQ.INV(0.05,\(\phi)\))」と入力して得られる値を採用します。
上側:「=CHISQ.INV.RT(0.05,\(\phi)\))」と入力して得られる値を採用します。
3-3. 一つの母分散の検定の実施例
事例1について、検定手順に従って検定してみましょう。
手順1. 帰無仮説\(H_0\)と対立仮説\(H_1\)を設定する。
母分散が従来より小さくなったかどうかを知りたいので、左片側検定で帰無仮説と対立仮説を設定します。
\(H_0:\sigma^2=\sigma^2_0\) (\(\sigma^2_0=0.50^2\))
\(H_1:\sigma^2 < \sigma^2_0\)
手順2. 有意水準\(\alpha\)を決める。
\(\alpha=0.05\)
手順3. 棄却域を決める。
棄却域:\(\chi^2_0 \le \chi^2(9,0.05)=3.33\)
\((\phi=n-1=10-1=9)\)
手順4. 検定統計量\(\chi^2_0\)の値を計算する。
得られたデータより、
\(S=0.5690\) (Excelの「DEVSQ」関数で求められる)
\(\chi^2_0=\displaystyle \frac{S}{\sigma^2_0}=\frac{0.5690}{0.50^2}=2.276\)
手順5. 判定する。
\(\chi^2_0=2.276 \le \chi^2(9,0.05)=3.33\)で検定統計量\(\chi^2_0\)は棄却域に入るので有意です。
よって帰無仮説\(H_0\)を棄却して、新ライン製造品の有効成分の量の母分散\(\sigma^2\)は、従来ラインの母分散\(0.50^2\)より小さくなったと判断できます。
4. 一つの母分散に関する推定
以前の記事で解説した通り、母分散\(\sigma^2\)の推定も点推定と区間推定の2種類があります。
4-1. 一つの母分散の推定手順
点推定はデータの分散\(V=\displaystyle \frac{S}{n-1}\)を使えばよいです。
区間推定については、基本事項から\(\chi^2=\displaystyle \frac{S}{\sigma^2}\)は自由度\(\phi=n-1\)の\(\chi^2\)分布に従うことから、以下が成立します。
\(Pr \left(\chi^2(\phi,1-\alpha/2)<\displaystyle \frac{S}{\sigma^2}<\chi^2(\phi,\alpha/2) \right)=1-\alpha\)
これを変形すると、以下のようになります。
\(~~Pr \left ( \displaystyle \frac{S}{\chi^2(\phi,\alpha/2)} <\sigma^2<\displaystyle \frac{S}{\chi^2(\phi,1-\alpha/2)} \right )\)
\(~~=1-\alpha \)
左項の括弧内の\(\sigma^2\)の範囲が、信頼率\(1-\alpha \)の信頼区間です。
一つの母分散の推定手順をまとめると、以下のようになります。
点推定:
\(\hat{\sigma}^2=V\) (Excelの「DEVSQ」関数で求められる)
区間推定:信頼率\(1-\alpha\)の信頼区間
\( \left (\displaystyle \frac{S}{\chi^2(\phi,\alpha/2)} , \displaystyle \frac{S}{\chi^2(\phi,1-\alpha/2)}\right )\)
4-2. 一つの母分散の推定の実施例
事例1について、点推定と区間推定を行ってみましょう。
点推定:
\(\hat{\sigma}^2=V=0.06322=0.251^2\)
区間推定:信頼率95%の信頼区間を求めます。
\( \left (\displaystyle \frac{S}{\chi^2(9,0.025)} , \displaystyle \frac{S}{\chi^2(9,0.975)}\right )\)
\( =\left (\displaystyle \frac{0.5690}{19.02} , \displaystyle \frac{0.5690}{2.70}\right )\)
\( =(0.02992, 0.2107)\)
\( =(0.173^2, 0.459^2)\)
5. 実践のためのアドバイス
モノづくりにおいては、特性値のばらつきに着目することはとても重要で、通常は工程能力指数で規格値に対する余裕度を判断します。
工程能力指数の算出には母分散が必要なので、母分散が基準値と比べて変化しているかどうか、あるいは母分散はどの程度かを検定や推定したい場面は多いでしょう。
そのときは、今回の\(\chi^2\)分布を使った検定と推定を使ってください。
6. おわりに
今回は、一つの母分散の検定と推定について解説しました。
一つ母分散の検定と推定では、左右非対称の\(\chi^2\)分布を使うので、棄却限界値を求めるときに注意が必要ですが、基本的な考え方と手順は変わりません。
工程能力を改善するためにはばらつきの低減が必要なので、対策の効果の有無を確認するときに、母分散の検定と推定を使うとよいでしょう。





