基本統計量の記事で、分散について説明しました。
分散とは、ばらつきを表す指標でしたね。
 データ分析の第一歩:基本統計量の活用方法
データ分析の第一歩:基本統計量の活用方法
今回は、分散の性質の一つである分散の加法性に着目して、その詳細と応用について解説します。
1. 分散の加法性とは
分散とはデータのばらつきを表す指標でした。
 データ分析の第一歩:基本統計量の活用方法
データ分析の第一歩:基本統計量の活用方法
分散にはいくつかの性質がありますが、その中で特に重要なものの一つが、「分散の加法性」と呼ばれる性質です。
分散の加法性とは、独立した2つの分布を足し合わせた分布の分散は、それぞれの分散を足し合わせた値に等しい、という性質です
1-1. 分散の加法性の具体例
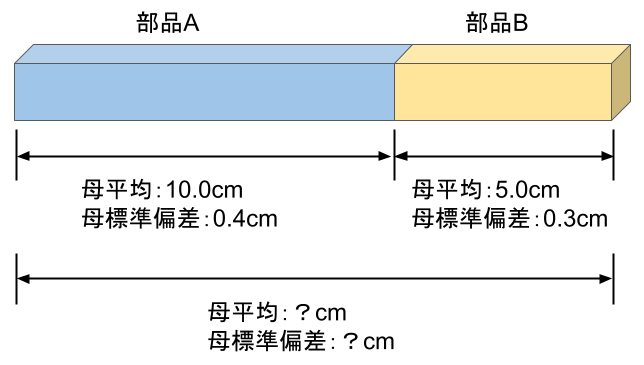
ある製品は、部品Aと部品Bを溶接して作っています。
過去の実績から部品Aの長さは母平均10.0cm、母標準偏差0.4cmの正規分布に、部品Bの長さは母平均5.0cm、母標準偏差0.3cmの正規分布に従うことが分かっています。
部品Aと部品Bをランダムに選んで溶接して製品を作るとき、製品の長さの母平均と母標準偏差はいくつになるでしょうか?
【解答例】
単純に部品Aと部品Bの母平均を足せば、製品の母平均を求められます。
母標準偏差は足し算で求めることはできませんが、2乗すれば母分散になるので、分散の加法性を利用して分散を求めてからルートを取ることで求められます。
製品の母平均 \(\mu=10.0+5.0=15.0cm\)
製品の母分散 \(\sigma^2=0.4^2+0.3^2=0.25cm^2\)
製品の母標準偏差 \(\sigma=\sqrt{0.25}=0.5cm\)
事例1は2つの分布の組み合わせでしたが、3つ以上の分布を組み合わせる場合でも、分散の加法性が成立するので、各分布の母分散を単純に足し合わせば組み合わせ後の母分散を求められます。
1-2. 分散の加法性に関する注意事項
分散の加法性を適用するにあたり、いくつか注意事項があります。
1) 分散を引き算することはない
どのような場合でも、2つの分布を組み合わせたときの母分散は足し合わさなければなりません。
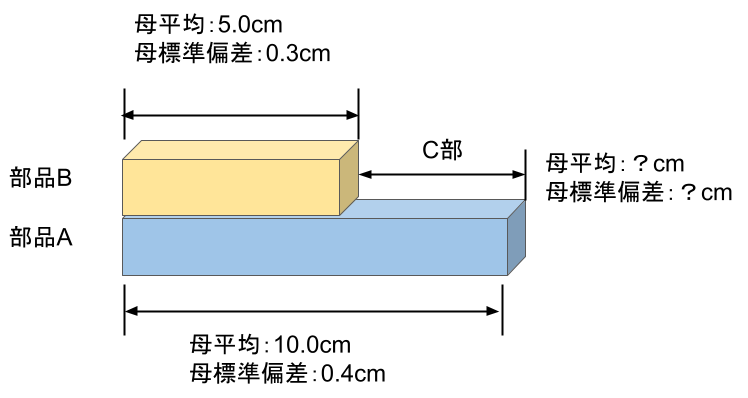
ある製品は、部品Aと部品Bを溶接して製造されています。
過去の実績から部品Aの長さは母平均10.0cm、母標準偏差0.4cmの正規分布に、部品Bの長さは母平均5.0cm、母標準偏差0.3cmの正規分布に従うことが分かっています。
部品Aと部品Bをランダムに選んで溶接して製品を作るとき、製品C部の長さの母平均と母標準偏差はいくつになるでしょうか?
【解答例】
単純に部品Aの母平均から部品Bの母平均を引けば、製品の母平均を求められます。
母平均を引き算で求めたので、母分散も引き算をしたくなりますが、それは誤りです。
あくまで2つの分布を組み合わせているので、分散の加法性に基づいて分散は足し合わさなければなりません。
製品の母平均 \(\mu=10.0-5.0=5.0cm\)
製品の母分散 \(\sigma^2=0.4^2+0.3^2=0.25cm^2\)
製品の母標準偏差 \(\sigma=\sqrt{0.25}=0.5cm\)
もし引き算が成り立つとすると、母分散が負の値になることがあるので、母分散の引き算は誤りであることが理解できます。
2) 組み合わせる分布はお互いに独立であること
分散の加法性が成り立つのは、お互いの分布が無関係で独立しているときだけです。
独立とは、2つの事象について片方の事象が変化したとき、もう片方の事象が変化しない状態を指します。
金属プレートから2枚の部品をくり抜き、重ね合わせた製品を作る例をを考えてみましょう。
1枚のシートからくり抜いた2つの部品を組み合わせるような場合が該当します。
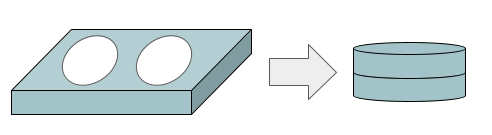
お互いの部品は同じシートから得られているので、重さや厚さなどの平均や標準偏差は関係があります。
このような場合、独立とは言いません。
1枚のシートからくり抜いた2つの部品を1つの箱に入れ、何個かたまってからランダムに取り出した2個の部品を組み合わせる場合。

2つの部品は異なるシートから得られているので、お互いに無関係です。
このような場合を独立と言い、分散の加法性が成立します。
2. 分散の加法性の応用
分散の加法性は、工業製品における公差設計でよく用いられる考え方です。
事例で見てみましょう。
あなたは、部品Aと部品Bを組み立てた製品の設計をしています。
部品A、Bは仕入先から購入しており、部品Aの寸法は\(16\pm0.18\)、部品Bの寸法は\(8\pm0.09\)で仕様書に記載されています。
でき上った製品は別の部品に組付けるため、製品寸法は\(24\pm0.25\)の規格を満たす必要があります。
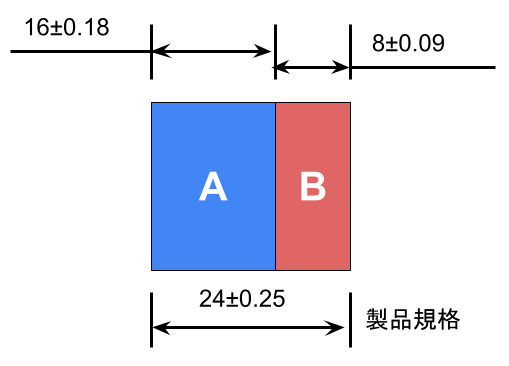
製品が規格を満足するか確認しましょう。
もし、規格を満足しない場合は、部品A、Bの寸法公差はいくつに設定しなければなりませんか?
【解答例】
良く用いられる公差の累積方法に、単純累積法と正規分布累積法があります。
それぞれの方法で解答を確認します。
2-1. 単純累積法の場合
単純累積法とは、単純に各部品公差の上限値と下限値を足し合わせて組立品の公差を決める方法です。
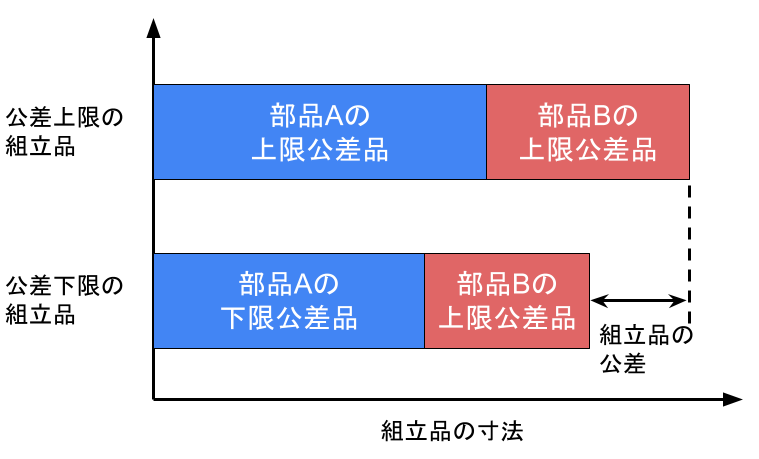
累積公差\(=\pm (x_1+x_2+\cdots+x_n)\)
ただし、\(x_n\)は各部品の公差です。
よって、
累積公差 \(=0.18+0.09=0.27\)
製品規格の公差0.25を上回っているので、規格を満足しません。
規格を満たすためには、規格を越える0.02を2つの部品に均等に割り振ると、各部品公差をさらに0.01厳しくする必要があります。
公差を厳しくするためには、一般的に加工精度の向上や選別などが必要となるため、部品のコストアップにつながる恐れがあります。
2-2. 正規分布累積法の場合
着目する特性が正規分布に従う場合、正規分布累積法を適用できます。
通常は規格の中心になるように作るので、規格の上限や下限に近い製品ができる確率は非常に小さいです。
ましてや、規格の上下限に近い部品同士が組み合わさる確率は非常に小さくなり、確率的には無視できるだろうと予想できます。
つまり、製品の寸法は、単純な公差の足し合わせよりも狭い範囲でばらつくと考えられます。
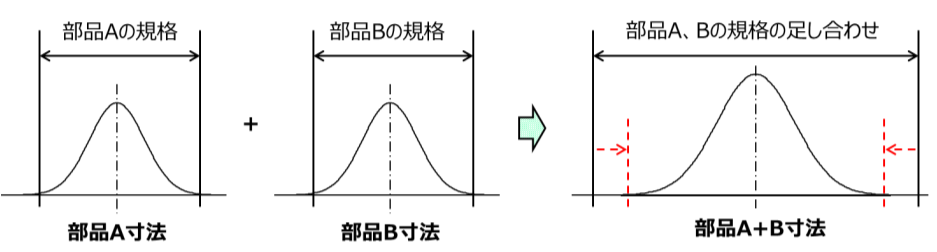
分散の加法性を利用して公差を決めることで、単純累積法よりも狭い範囲で公差を設定できます。
事例3について、分散の加法性を使って公差を求める以下のようになり、製品規格を満足します。
製品の寸法公差 \(=\pm \sqrt{0.18^2+0.09^2}=0.20<0.25\)
もし、各部品の寸法公差を\(\pm3\sigma\)と仮定すれば、99.7%以上の確率で製品規格を満足すると言えます。
このように、正規分布累積法を使えば、単純累積法よりも公差をゆるく設定できるので、部品の寸法精度アップなどの過剰な対策は不要となり、コスト低減が可能となります。
ただし、ばらつきが大きくなったり、平均値が大きくずれたりすると、規格上下限付近の出現確率が上がり、確率的にはあり得なかった組み合わせが多発することになります。
したがって、正規分布累積法を適用して公差を設定する場合は、平均値とばらつきの管理をしっかり行う必要があります。
3. 実践のためのアドバイス
分散の加法性は、公差設計において重要な位置を占めています。
ただし、組み合わせによっては分散の加法性を適用できない場合があるので、そのときは乱数を発生させて組み合わせたあとの分散を計算するなど、工夫が必要です。
分散の加法性を適用してよい場面かどうかを確認してから、分散の加法性を使ってください。
4. おわりに
今回は、分散の性質の一つである分散の加法性について解説しました。
分散の加法性は、複数の部品を組み合わせたときのばらつきを見積もるときなどによく用いられ、公差設計にも応用される基本的なルールです。
ただし、分散の加法性はデータが正規分布に従うことが前提なので、分散の加法性を適用する前に、ヒストグラムを作成して正規分布に従うとみなせるかを、事前によく確認してください。








