前回、2つの変数\(x\)と\(y\)に関して、\(y\)を\(x\)で予測するための回帰式を求める回帰分析について解説しました。
 2変数の関係を表すモデル式を求める~単回帰分析①~
2変数の関係を表すモデル式を求める~単回帰分析①~
ただし、データから求めた単回帰式を見ただけでは、単回帰式がどれだけ精度良く\(x\)で\(y\)を説明できているかの適合度(予測精度)が分かりません。
そこで、今回は得られた単回帰式の評価方法および、単回帰分析における注意点を解説します。
1. 総平方和の分解
個々のデータ\(y_i\)とデータの\(y\)の平均値\(\bar{y}\)の差\((y_i-\bar{y})\)を総変動、予測値\(\hat{y}_i\)と\(\bar{y}\)の差\((\hat{y}_i-\bar{y})\)を回帰変動、\(y_i\)と\(\hat{y}_i\)の差\((y_i-\hat{y}_i)\)を残差\(e_i\)とすると、それぞれの関係は以下の図のように表せます。
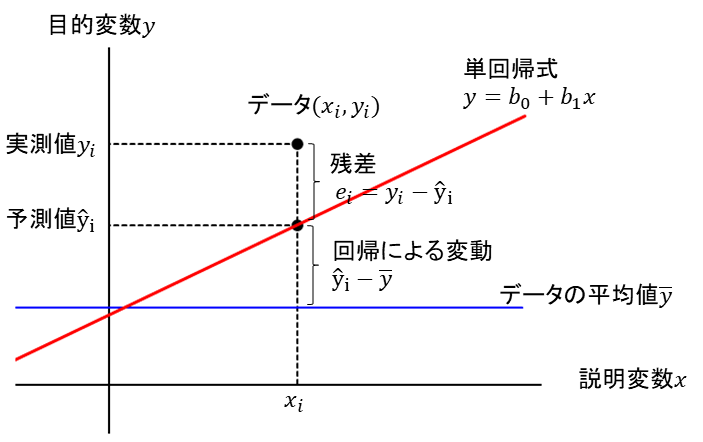
すべてのデータについて考えると、総平方和\(S_{yy}=\sum_{i=1}^{n}(y_i-\bar{y})^2\)は、回帰変動の平方和\(S_R\)と残差平方和\(S_e\)に分解できます。
$$S_{yy}=\displaystyle \sum_{i=1}^{n}(y_i-\bar{y})^2=\sum_{i=1}^{n}(\hat{y}_i-\bar{y})^2+\sum_{i=1}^{n}(y_i-\hat{y}_i)^2=S_R+S_e$$
ここで、回帰変動の平方和\(S_R\)は以下のように変形できます。
\(S_R=\displaystyle \sum_{i=1}^{n}(\hat{y}_i-\bar{y})^2=\sum_{i=1}^{n}\lbrace \bar{y}+b_1(x_i-\bar{x})-\bar{y}\rbrace ^2\)
\(\qquad =b_1^2 \displaystyle \sum_{i=1}^{n} (x_i-\bar{x})^2=b_1^2S_{xx}=b_1\frac{S_{xy}}{S_{xx}}S_{xx}=b_1S_{xy}\)
2. 寄与率の算出
さて、総平方和を分解することにより、求めた回帰式の適合度(精度)の指標である寄与率(決定係数)\(R^2\)を以下の式から求められます。
寄与率:\(R^2=\displaystyle \frac{S_R}{S_{yy}}=\frac{S_{yy}-S_e}{S_{yy}}=1-\frac{S_e}{S_yy}\)
\(R^2\)は通常は0から1の範囲を取り、1に近いほど回帰式の適合度が高いことを意味します。
ただし、適合度があまりに低いと、寄与率がマイナスになることがあります。
これは、単にデータの\(\bar{y}\)を用いただけの回帰式\(y=\bar{y}\)より、求めた回帰式の適合度が悪いときに起こり得ます。
また、寄与率の代わりに自由度調整済み寄与率(自由度調整済み決定係数)\(R^{*2}\)を使う場合があります。
単回帰分析では、寄与率と自由度調整済み寄与率の間に差はあまりないので寄与率で適合度を見ればよいですが、説明変数が2つ以上の重回帰分析では、重回帰式に取り込む説明変数が多いほど寄与率は大きくなる傾向があるので、それを補正するために自由度調整済み寄与率がよく用いられます。
自由度調整済み寄与率:\(R^{*2}=1-\displaystyle \frac{S_e/\phi _e}{S_{yy}/\phi_{yy}}\)
ただし、
\(\phi_{yy}=n-1\):総平方和の自由度
\(\phi_e=n-2\):残差平方和の自由度
自由度調整済み寄与率の詳細は、重回帰分析の記事で改めて解説します。
求めた単回帰式の適合度の評価は、機械学習で得られるさまざまなモデルの適合度を評価するプロセスと全く同じです。
機械学習に携わる方はまずはシンプルな単回帰分析で、考え方を理解してください。
3. 単回帰分析を行う際の注意事項
単回帰分析は非常にシンプルで基本的な解析方法ですが、使い方を誤ると間違った判断に至る可能性があります。
そこで、単回帰分析で行いがちな過ちを2点紹介しますので、実務で誤った使い方をしないように気を付けてください。
3-1. 外挿は行わないこと
単回帰分析でやりがちな過ちは外挿です。
外挿とは、取得したデータを基にして、取得データの範囲外で予測値を求めることです。
単回帰式を得られると、単回帰式の\(x\)にどんな値を入れても予測値\(\hat{y}\)が得られるので、取得データを無視して予測値を求めがちです。
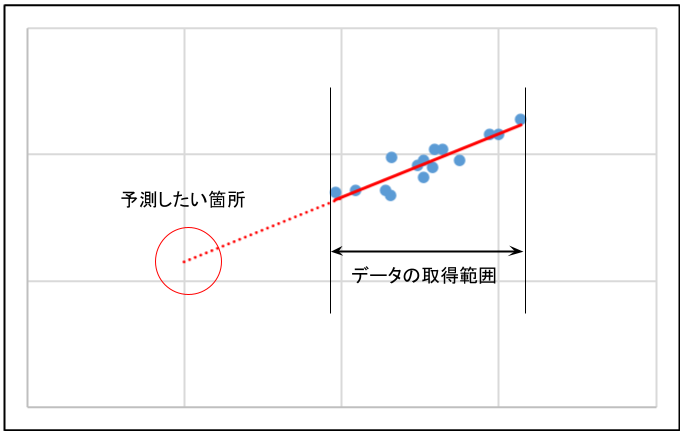
しかし、直線関係があるのはあくまで取得データの範囲内であって、その外側も直線関係が成り立つかは全く分かりません。傾向が大きく変わって、予測値と実測値に大きな乖離が生じることもあり得ます。
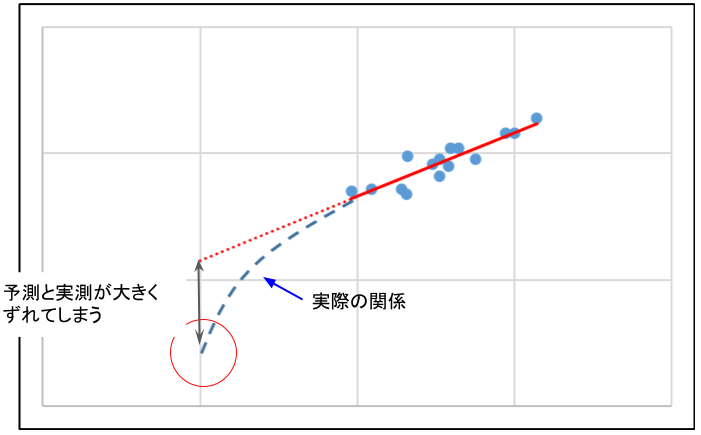
安易に外挿で予測するのではなく、見たい領域のデータを採取して直線性の有無を確認しましょう。
3-2. データのばらつきを考慮すること
製造業では、特性が規格に入るように製造条件を決めたいといったように、結果系から要因系を予測したい場面がよくあります。
単回帰式が求まれば、\(y\)に値を代入すれば\(x\)の値が求まるので、規格の上下限を\(y\)に代入することで\(x\)の上下限を決められるのではと思いがちです。
\(x\)と\(y\)の相関係数が1または-1であれば、完璧に一直線上にデータが並んでいることを意味しており、\(y\)と回帰直線との交点から\(x\)の上下限を求めても問題ありませんが、実際は回帰直線の周りにばらつきがあるので、そのばらつきを考慮して\(x\)の上下限を決める必要があります。
事例2で具体的な考え方を説明します。
条件\(x\)と特性\(y\)について、以下のデータが得られました。
特性\(y\)の規格が2.25以上3.05以下の時、規格を満足するように条件\(x\)の管理幅を決めましょう。
| No. | 条件\(x\) | 特性\(y\) |
|---|---|---|
| 1 | 56 | 3.72 |
| 2 | 58 | 3.52 |
| 3 | 60 | 3.10 |
| 4 | 62 | 2.86 |
| 5 | 63 | 2.80 |
| 6 | 64 | 2.70 |
| 7 | 66 | 2.58 |
| 8 | 68 | 2.21 |
散布図を作成すると条件\(x\)と特性\(y\)には直線関係が見られ、単回帰式は以下のように求まります。
$$y=10.508-0.122\times x$$
相関係数\(r=-0.988\)と直線に近い関係ですが、完全に直線には乗らず、データは回帰直線の周りでばらつきを持ちます。
データがばらつく範囲を95%予測区間で求めることが多いので、95%予測区間(母集団から100回データを取ったとき、95回が含まれる範囲)を求めて散布図にプロットしてみます。
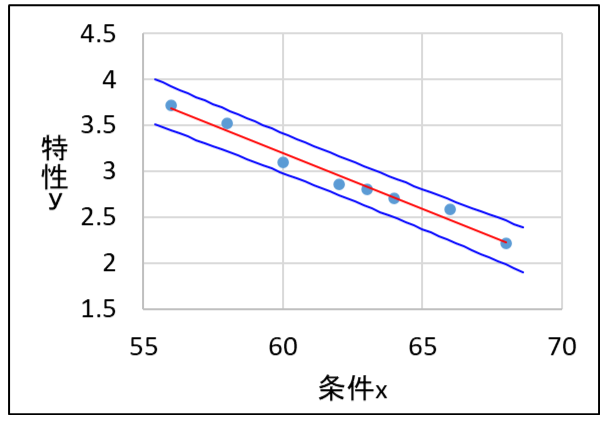
なお、95%予測区間は以下のように求められます。
95%予測区間\(=(b_0+b_1x)\pm t(n-2,0.05)\sqrt{\left \lbrace 1+\displaystyle \frac{1}{n}+\frac{(x-\bar{x})^2}{S_{xx}} \right \rbrace V_e}\)
ただし、\(t(n-2,0.05)\)は\(t\)分布における\(t\)値
\(V_e=\displaystyle \frac{S_{yy}-\displaystyle \frac{S_{xy}^2}{S_{xx}}}{n-2}\)
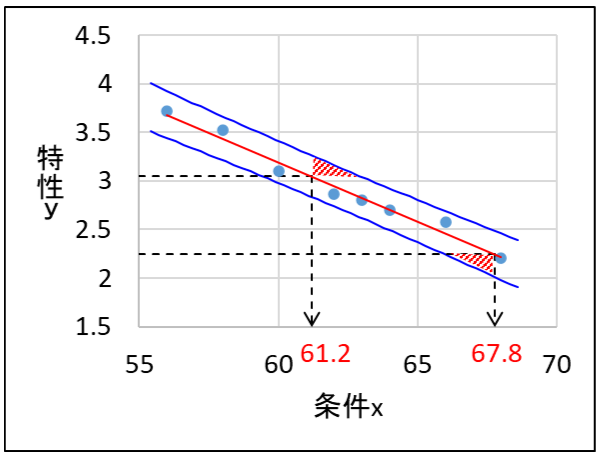
ここで、規格値と回帰直線との交点から条件\(x\)の管理値を決めるとどうなるでしょうか?
単回帰式の\(y\)に規格値を代入して\(x\)を求めると、61.2~67.8が規格を満足する範囲と求められますが、ばらつきを考えると下図の斜線部分が規格外れとなる恐れがあります。
したがって、特性\(y\)の規格外れ品が発生しないようにするためには、ばらつきを考慮して、つまり、特性\(y\)の規格値と予測区間との交点から条件\(x\)の範囲を決める必要があります。
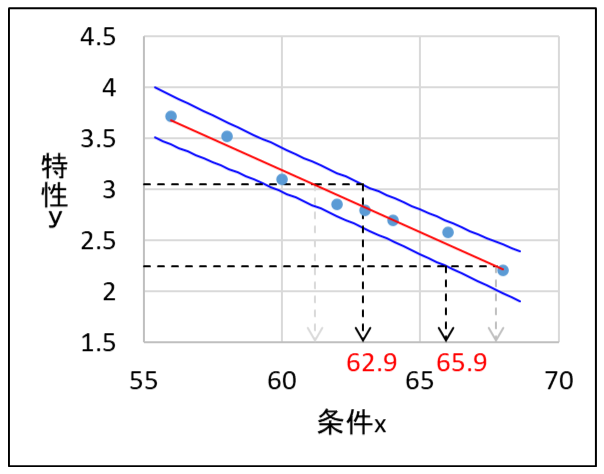
特性\(y\)の規格値と予測区間の交点から条件\(x\)の範囲を求めると62.9~65.9となり、この範囲で条件\(x\)を設定すれば、ばらつきを考慮しても特性\(y\)の規格外れ品が生じないと推定できます。
このように、単回帰分析の結果を使って要因系の管理幅を決めたいときは、必ず回帰直線周りのばらつきを考慮して設定してください。
4. おわりに
今回は、単回帰式の適合度の評価方法と、単回帰分析を適用するにあたって注意すべき点を解説しました。
単回帰分析を行うと単回帰式が得られますが、単回帰式がデータによく適合しているかを評価し、適合度が高ければ単回帰式を使って精度の高い予測が可能となります。
また、単回帰式を使った予測するときは、取得したデータの範囲内でばらつきを考慮することが必要です。
単回帰分析で単回帰式は簡単に求まりますが、その活用方法には十分に注意してください。






