前回と前々回の記事で、2つの変数の相関関係を分析する相関分析を見てきました。
散布図を作成し、相関係数を求めることで2つの相関の強さを定量化できました。
相関分析により相関が強い、つまり、直線関係が強いことが分かると、結果系\(y\)を要因系\(x\)で説明あるいは予測したいというニーズが生まれます。
このようなときに役に立つ手法が、単回帰分析です。
今回は単回帰分析について解説します。
1. 単回帰分析とは
回帰分析とは、要因系の変数\(x\)と結果系の変数\(y\)について、\(y=f(x)\)という関係式を当てはめて、\(y\)を\(x\)で説明したり、\(x\)の値から\(y\)を予測したりする分析方法です。
回帰分析では、要因系の\(x\)を説明変数(独立変数)、結果系の\(y\)を目的変数(従属変数)と言います。
回帰分析の最もシンプルなモデルは、説明変数が1つのみの一次式のモデルで、この場合の分析方法を単回帰分析と言います。
相関分析で取り上げた事例1で単回帰分析を行ってみます。
以下のデータは、ある製品の長さと重量を測定したデータです。
| No. | 長さ(cm) | 重量(g) |
|---|---|---|
| 1 | 20.96 | 53.5 |
| 2 | 21.28 | 53.6 |
| 3 | 21.09 | 53.6 |
| 4 | 21.48 | 54.6 |
| 5 | 22.0 | 55.8 |
| 6 | 21.64 | 55.2 |
| 7 | 21.59 | 55.2 |
| 8 | 21.52 | 54.8 |
| 9 | 21.75 | 54.8 |
| 10 | 21.94 | 55.8 |
| 11 | 21.31 | 53.4 |
| 12 | 21.52 | 54.1 |
| 13 | 21.58 | 54.5 |
| 14 | 22.14 | 56.4 |
| 15 | 21.32 | 54.9 |
このデータについて散布図を作成し、直線を当てはめると以下のようになります。
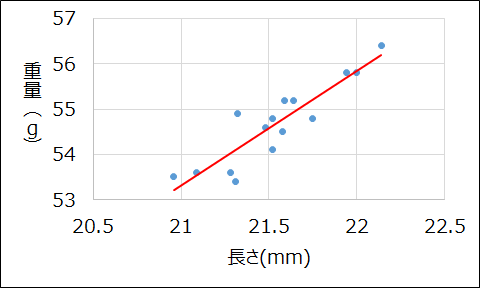
データの塊の真ん中付近を通るように直線が引かれています。
このような直線を求めるのが単回帰分析で、事例1の直線の式は、\(y = 2.5316x + 0.1459\)と表せます。
単回帰分析では、直線の式をのことを単回帰式と呼びます。
2. 単回帰式の求め方
それでは、単回帰式の求め方を詳しく見ていきましょう。
2-1. 単回帰分析で用いられる用語
単回帰分析の詳細に入る前に、単回帰分析でよく用いられる用語を解説します。
この後で、これらの用語を使って単回帰分析を詳しく説明しますので、まずは用語をしっかり理解してください。
説明変数\(x\)と目的変数\(y\)に関する2次元のデータ\((x_i,y_i)\quad (i=1, 2, \cdots,n)\)に対する単回帰式モデルは、以下のような一次式で表せます。
$$y_i=\beta_0+\beta_1x_i+\varepsilon$$
ただし、\(\beta_0\)は切片の母数、\(\beta_1\)は傾きの母数(母回帰係数)、\(\varepsilon_i\)は誤差項です。
\(\varepsilon_i\)はお互いに独立で、正規分布\(N(0,\sigma^2)\)に従うと仮定します。
限られたデータから母数を正確に推定するのは難しいので、与えられたデータから\(\beta_0\)と\(\beta_1\)の推定値\(b_0\)、\(b_1\)を求めることが回帰分析に該当します。
\(b_0\)と\(b_1\)に基づく一次式は以下のように表され、この一次式のことを単回帰式と言います。
$$y=b_0+b_1x$$
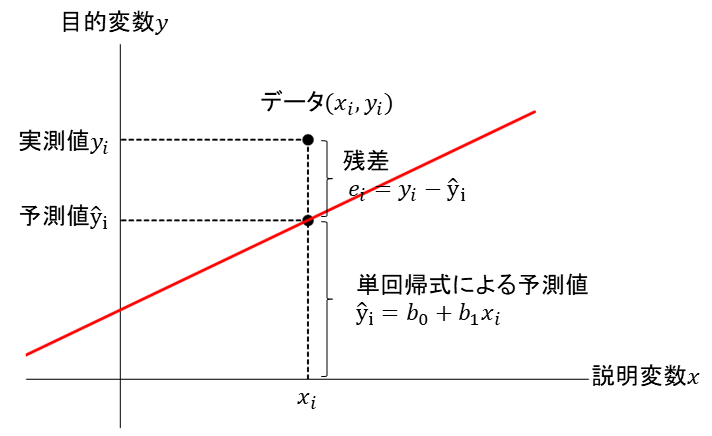
この式から、実測値\(y_i\)の予測値\(\hat {y}_i\)は以下のように表せます。
$$\hat{y}_i=b_0+b_1x_i \qquad(i=1, 2, \cdots,n)$$
このとき、予測値\(\hat {y}_i\)と実測値\(y_i\)の差を残差\(e_i\)と言います。
\(\hat {y}_i\)の式を用いると、残差\(e_i\)は以下のように表せます。
$$e_i=y_i-\hat {y}_i=y_i-(b_0+b_1x_i) \qquad(i=1, 2, \cdots,n)$$
これまで出てきた、単回帰式、予測値、実測値、残差の関係をまとめたものが以下の図です。
2-2. 単回帰式の求め方
それでは、単回帰分析において単回帰式をどのように求めればよいでしょうか。
データが完全に一直線上に並べば、残差は全く生じず、単回帰式も容易に求められます。
しかし、実際はデータはばらつくので、どのように回帰直線を引いても残差は生じることになります。
従って、残差が最小になるように引いた回帰直線が、最も精度の高い直線であり、その回帰直線を表す一次式がよい単回帰式ということになります。
プロットは複数ありますが、単純に各プロットの残差の合計が最小になるように回帰式を決めようとしてもうまくいきません。
なぜなら、回帰直線と実測値の差である残差の合計は必ず0になるからです。
そこで、各プロットの残差の2乗を合計した残差平方和\(S_e\)が最小になるように、回帰式の\(b_0\)と\(b_1\)を求めます。
残差平方和:\(S_e=\displaystyle \sum_{i=1}^{n}e_i^2=\sum_{i=1}^{n}(y_i-\hat{y}_i)^2=\sum_{i=1}^{n}{y_i-(b_0+b_1x_i)}^2\)
残差平方和\(S_e\)が最小になるように\(b_0\)と\(b_1\)を決める方法を、最小2乗法と言います。
具体的には、\(S_e\)を\(b_0\)と\(b_1\)で偏微分してそれを0とおきます。
\(\displaystyle \frac{\partial S_e}{\partial b_0} =\sum_{i=1}^{n}\frac{\partial}{\partial b_0}{y_i-(b_0+b_1x_i)}^2\)
\(\qquad =\displaystyle \sum_{i=1}^{n}2\lbrace y_i-(b_0+b_1x_i)\rbrace (-1)\)
\(\qquad=-2\displaystyle \sum_{i=1}^{n}\lbrace y_i-(b_0+b_1x_i) \rbrace=0\)
\(\therefore nb_0+b_1\displaystyle \sum_{i=1}^{n}x_i=\sum_{i=1}^{n}y_i \quad (1)\)
\(\displaystyle \frac{\partial S_e}{\partial b_1} =\sum_{i=1}^{n}\frac{\partial}{\partial b_1}\lbrace y_i-(b_0+b_1x_i)\rbrace ^2\)
\(\qquad=\displaystyle \sum_{i=1}^{n}2\lbrace y_i-(b_0+b_1x_i) \rbrace(-x_i)\)
\(\qquad=-2\displaystyle \sum_{i=1}^{n}\lbrace y_i-(b_0+b_1x_i)\rbrace \cdot x_i=0\)
\(\therefore b_0\displaystyle \sum_{i=1}^{n}x_i+b_1 \sum_{i=1}^{n}x_i^2=\sum_{i=1}^{n}x_iy_i \quad (2) \)
得られた2つの式(1)(2)を連立方程式とし、\(b_0\)と\(b_1\)を求めます。
式(1)を変形すると式(3)が得られます。
$$b_0=\frac{1}{n} \displaystyle \sum_{i=1}^{n}y_i-b_1\cdot \frac{1}{n}\sum_{i=1}^{n}x_i=\bar{y}-b_1\bar{x} \tag{3}$$
式(3)を式(2)に代入すると式(4)が得られます。
\begin{align}
\left (\frac{1}{n} \displaystyle \sum_{i=1}^{n}y_i-b_1\cdot \frac{1}{n}\sum_{i=1}^{n}x_i \right ) \sum_{i=1}^{n}x_i+b_1 \sum_{i=1}^{n}x_i^2=\sum_{i=1}^{n}x_iy_i\\
\\
\left \lbrace \displaystyle \sum_{i=1}^{n}x_i^2-\frac{(\sum_{i=1}^{n}x_i)^2}{n} \right \rbrace b_1=\displaystyle \sum_{i=1}^{n}x_iy_i-\frac{(\sum_{i=1}^{n}x_i)(\sum_{i=1}^{n}y_i)}{n} \tag{4}
\end{align}
ここで、\(x\)の偏差平方和を\(S_{xx}\)、\(x\)と\(y\)の偏差積和を\(S_{xy}\)とすると、式(4)左辺の\(b_1\)の係数は\(S_{xx}\)、式(4)右辺は\(S_{xy}\)となるので、式(4)は以下のように整理できます。
$$S_{xx}b_1=S_{xy}\quad \Rightarrow \quad b_1=\displaystyle \frac{S_{xy}}{S_{xx}}$$
以上をまとめると、単回帰式\(\hat{y}=b_0+b_1x\)の\(b_0\)と\(b_1\)は以下のように表せます。
傾き:\(b_1=\displaystyle \frac{S_{xy}}{S_{xx}}\) 切片:\(b_0=\bar{y}-b_1\bar{x}\)
2-3. 単回帰式の導出例
2-2で単回帰式の求め方を見ましたので、事例1について単回帰式を求めてみましょう。
まずは、回帰式の導出に必要な統計量を求めます。
\(n=15\)
\(\displaystyle \sum_{i=1}^{n}x_i=323.12,\quad \sum_{i=1}^{n}x_i^2=6961.9376\)
\(\displaystyle \sum_{i=1}^{n}y_i=820.2,\quad \sum_{i=1}^{n}y_i^2=44860.36\)
\(\displaystyle \sum_{i=1}^{n}x_iy_i=17672.004,\quad \bar{x}=\displaystyle \frac{1}{n}\sum_{i=1}^{n}x_i=\frac{323.12}{15}=21.541\)
\(S_{xx}=\displaystyle \sum_{i=1}^{n}x_i^2-\frac{(\sum_{i=1}^{n}x_i)^2}{n}=6961.9376-\frac{(323.12)^2}{15}=1.501973\)
\(\bar{y}=\displaystyle \frac{1}{n}\sum_{i=1}^{n}y_i=\frac{820.2}{15}=54.68\)
\(S_{xy}=\displaystyle \sum_{i=1}^{n}x_iy_i-\frac{(\sum_{i=1}^{n}x_i)(\sum_{i=1}^{n}y_i)}{n}=17672.004-\frac{323.12\times 820.2}{15}=3.8024\)
これらを使って、単回帰式の切片\(b_0\)と傾き\(b_1\)を求めます。
\(b_1=\displaystyle \frac{S_{xy}}{S_{xx}}=\frac{3.8024}{1.501973}=2.5316\)
\(b_0=\bar{y}-b_1\bar{x}=54.68-2.5316\times 21.541=0.1459\)
したがって、事例1の単回帰式は次のように求まります。
$$y=b_0+b_1x=0.1459+2.5316x$$
導出した単回帰式がどのくらい精度が高いのかの評価方法は、次の記事で解説します。

3. おわりに
今回は、単回帰分析の実施方法を解説しました。
単回帰分析は、2変数の関係を一次式で表す基本的な分析であるだけでなく、現在あちこちで研究されている機械学習の最も基本的なモデルでもあり、機械学習の入口とも言える解析方法です。
単回帰分析の考え方は応用の範囲がとても広いので、データ解析を行おうとしている方は確実に理解してください。




