計量値同士の関係を確認するのに使われるグラフが「散布図」です。
特に、要因系の変数と結果系の変数について、相互の関係(相関関係)があるかを確認したり、データ解析の際の事前確認などでよく作成します。
今回は散布図に着目して、散布図の作り方と見るポイントを解説します。
1. 散布図とは
散布図とは、対になった2つのデータの相互の関係(相関関係)を見える化するため、x軸とy軸の座標面にデータをプロットした図です。
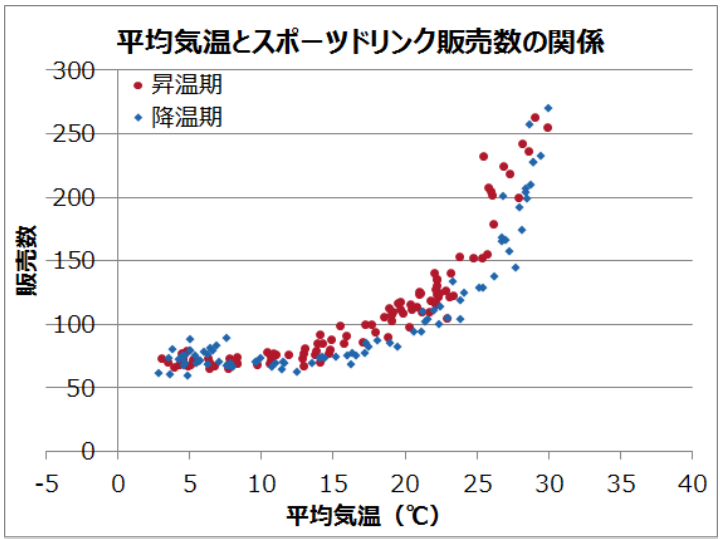
先の事例の場合、横軸が平均気温、縦軸がスポーツドリンクの販売数であり、気温が上昇すると販売数も増えることがひと目で把握できます。
2. 散布図の基本
散布図の基本を簡単に解説します。
2-1. データの種類
散布図を作るには対になった2つのデータが必要ですが、組み合わせは以下の3つのいずれかになります。
| 組み合わせの種類 | 概要 | 具体例 |
|---|---|---|
| 要因系と結果系 | ある結果と、それに影響を与えると考えられる要因の関係 | テスト勉強の時間(要因)とテストの点数(結果) |
| 結果系と結果系 | 2つの結果の関係 | 国語のテストの点数(結果)と数学のテストの点数(結果) |
| 要因系と要因系 | ある結果に影響を与えると考えられる2つの要因の関係 | テスト勉強の時間(要因)と遊んでいた時間の関係(要因) |
散布図を作成する前に、対になったデータがどんな組み合わせなのかを把握しましょう。
2-2. 散布図作成のメリット
散布図を作成すると、以下のメリットがあります。
1) 結果系のばらつきに影響を与える要因系を把握できます。
2) 要因系と結果系の関係の有無を把握できます。
別の機会に解説する回帰分析を行えば、目標とする結果にするには要因系の数値をいくつにすればよいか、といった予測が可能となります。
3) 結果系の測定が難しい場合、あるいは、壊さないと結果系のデータが得られない場合、本来見たい結果の代わりとなる代用特性を探索できます。
例えば、本当は特性Aを測定したいが、特性Aを求めるには製品を壊さないといけないので、常に測定するのは難しい。
そこで、散布図を描いたところ、特性Aと相関の強い特性Bという簡単に測定できる特性を見つけられたので、特性Bを測定することで特性Aを保証できるようになった、といった例です。
このとき、特性Bを特性Aの代用特性と言います。
3. 散布図の作り方
手順1. 対になった2つのデータを収集する。
対応する2つのデータを収集し、xとyとします。
要因系と結果系のデータの場合は、要因系をx、結果系をyとしてください。
関係を正しく把握するために、最低30組のデータを収集することが望ましいです。
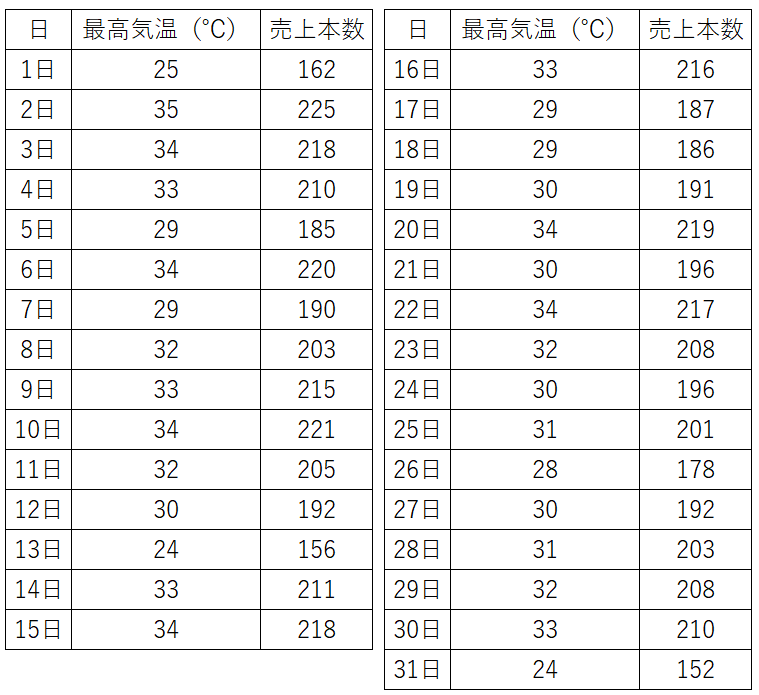
下の表は、7月の各日の最高気温とあるお店のビールの売上本数をまとめた表です。
このデータを使って散布図を作ってみましょう。
手順2. 対になった観測値\((x, y)\)を座標平面上にプロットする。
事例のデータをExcelでプロットすると、以下のようになります。
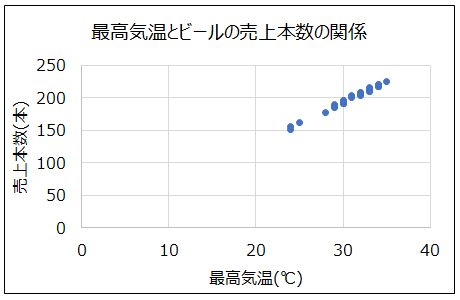
Excelで散布図を作成すると、縦軸と横軸の目盛りは自動で設定されますが、上のグラフのように、0から始まるように設定されると、プロットが隅に偏ってしまい見た目がよくありません。
手順3. xとyの最大値、最小値を求めデータがグラフいっぱいになるように、軸の目盛りを調整する。
事例の場合、最高気温は24~35℃、売上本数は152~225本なので、これを参考に軸の目盛りを決めます。
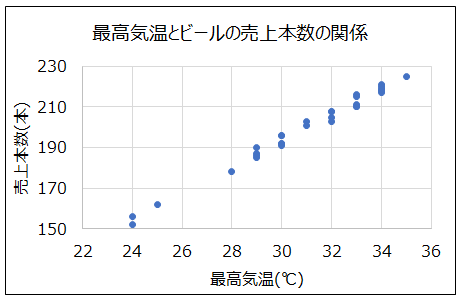
これで、散布図が完成です。
4. 散布図の見方
散布図にはさまざまなパターンがあるので、各パターンで何が言えるかを見ていきましょう。
| 散布図の形 | 特徴 |
|---|---|
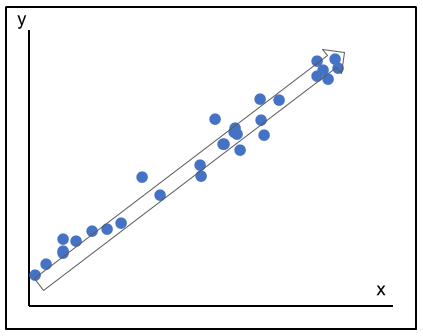 | 強い正の相関がある。 \(x\)が増加すれば、\(y\)も直線的に増加する。 |
 | 強い負の相関がある。 \(x\)が増加すると、\(y\)は直線的に減少する。 |
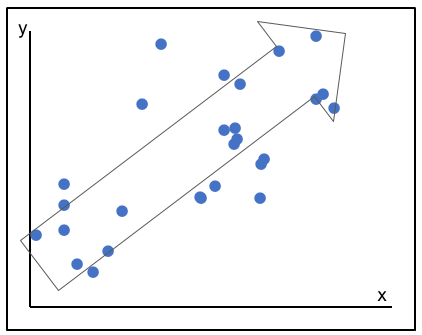 | 弱い正の相関がある。 \(x\)が増加すれば\(y\)も増加するがばらつきが大きい。 |
 | 弱い負の相関がある。 \(x\)が増加すれと\(y\)は減少するがばらつきが大きい。 |
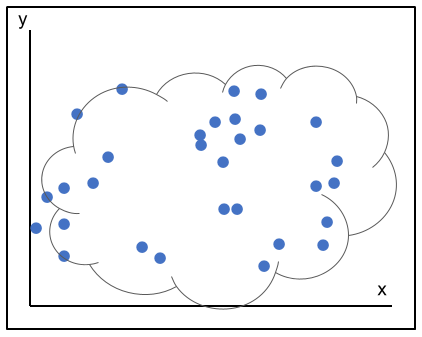 | 無相関である(相関関係がない)。 \(x\)と\(y\)に関係がなく、点が全体的に散らばっている。 |
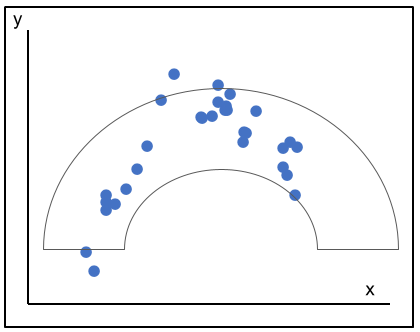 | 曲線関係がある。 \(x\)と\(y\)に2次の関係がある。 この場合、一般的に相関関係があるとは言わない。 |
相関関係の強さは相関係数\(r\)で表せますが、相関係数\(r\)の求め方などの詳細は、別の記事で解説します。

5. 実践のためのアドバイス
関係のありそうな2つ以上の計量値のデータを収集したら、散布図を作成するのが基本です。
Excelで散布図を描くとプロットが上下左右のいずれかに寄ってしまうことがあります。
このときは、軸の表示範囲を変更して、プロットが対角線上に並ぶようにすると、解釈しやすくなります。
6. おわりに
今回は、散布図について解説しました。
散布図は対になった2つのデータの関係を見える化するのに、非常によく使われます。
データ解析の際も、2変数間の相関の強さが解析結果に影響することもあり、解析前の事前チェックで散布図を作成するのが一般的です。
2変数の関係を見ることができる散布図は、確実に作成できるようにしてください。