製造業においては、寸法や特性に規格が設けられ、規格を外れないものづくりが求められます。
製造している製品が、規格に対して十分に余裕があるのかないのか、規格に対して余裕がなければ規格外れが生じないように改善するといった処置が必要です。
このような過程で必要な考え方が工程能力と、工程能力を数値化した工程能力指数です。
今回は、製造業でよく取り上げられる、工程能力の考え方と工程能力指数を解説します。
1. 工程能力とは?工程能力指数とは?
安定した製造工程などのプロセスが、規格(要求事項)に対して余裕を持って製品やサービスを提供できる能力を工程能力といいます。
工程能力が高ければ不良品ができにくく、工程能力が低ければ不良品ができやすい工程ということです。
工程能力を数値で定量化した指標を工程能力指数といい、工程能力指数が大きければ工程能力が高いと判断できます。
2. 工程能力指数の求め方
ある製品を作っている工程を想像してください。
製品の特性を測定すると、そのデータは必ずばらつくのでデータの分布が得られます。
規格に対して分布の中心が偏っていたり、ばらつきが大きかったりしたら、規格外れが生じやすいことが想定できます。
工程の状態を数値で表した指標が工程能力指数で、工程能力指数には分布の中心を考慮しない\(C_p\)と、分布の中心を考慮する\(C_{pk},C_{pkL},C_{pkU}\)があります。(この表記は、日本産業規格JIS Z 8101-2に準拠しています。)
| 工程能力指数 | 特徴 | 得られる情報 |
|---|---|---|
| \(C_p\) | 分布のばらつきのみを考慮する | 規格幅に対する余裕度 |
| \(C_{pk},C_{pkL},C_{pkU}\) | 分布の中心とばらつきを考慮する | 規格外品発生のリスク |
2-1. 工程能力指数\(C_p\)とは
規格幅に対応した工程能力を表した指標で、分布のばらつき\((\pm3\sigma=6\sigma)\)と規格幅を比較した数値です。
分布のばらつきが規格幅に対して余裕があるかを判断できます。
| 規格幅に対してばらつきが小さい工程 | 規格幅に対してばらつきが大きい工程 |
|---|---|
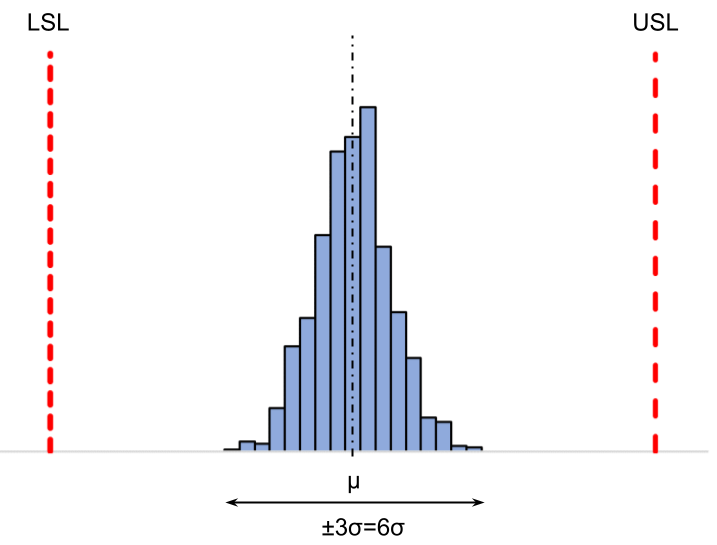 | 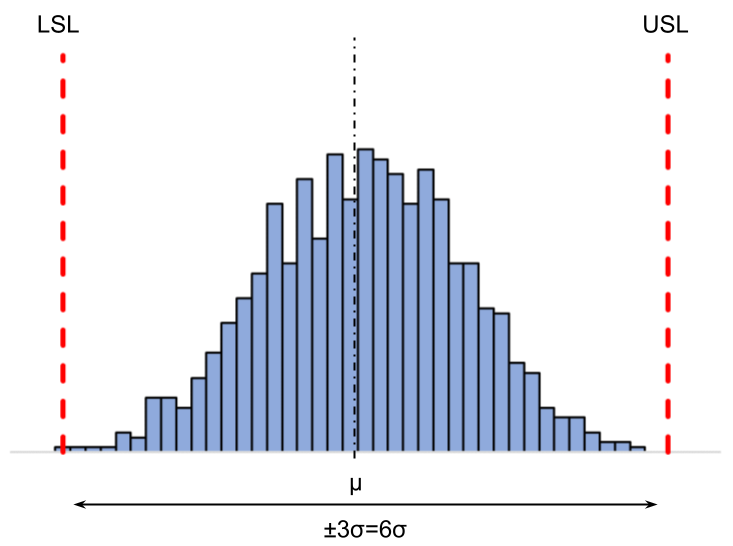 |
| 工程能力がある状態(\(C_p\)大) 分布の平均が何らかの要因で変化しても、規格を外れにくい。 | 工程能力がない状態(\(C_p\)小) 分布の平均が何らかの要因で変化すると、規格外れが多発する恐れがある。 |
\(\mu\):母平均 \(\sigma\):母標準偏差 \(USL\):規格上限 \(LSL\):規格下限
2-2. 工程能力指数\(C_p\)の計算方法と工程能力の評価
工程能力指数\(C_p\)は、以下の式で算出できます。
$$C_p=\frac{USL-LSL}{6\sigma}=\frac{規格幅}{6×母標準偏差}$$
得られた\(C_p\)の値により、工程能力を以下のように判断します。
なお、判断基準はルール化されているわけではないので、あくまで目安と考えてください。
| \(C_p\)の値 | 工程能力の評価 |
|---|---|
| \(1.33\le C_p\) | 規格幅に対して余裕があり、工程能力は十分ある状態 |
| \(1.0\le C_p \lt 1.33\) | 規格幅に余裕はあるものの、ばらつきの増加に注意が必要な状態 |
| \(C_p \lt 1.0\) | 規格幅に対して余裕がなく、工程能力は不足している状態 |
\(C_p\)が1.33であれば、規格幅は分布の\(\pm4\sigma\)相当ということになり、規格幅に対して特性のばらつきが十分に小さいと判断することが一般的です。
ある製品の特性の上限規格は\(USL=54\)、下限規格は\(LSL=30\)です。
特性のデータが十分にあり、母標準偏差\(\sigma=2\)のとき、工程能力指数\(C_p\)を求めて工程の状態を判断しましょう。
【解答例】
$$C_p=\frac{54-30}{6 \times 2}=2.0$$
\(C_p\)は1.33を上回っており、規格幅に対して特性のばらつきは小さく、工程能力は十分と判断できます。
2-3. 工程能力指数\(C_{pk}\)とは
工程能力指数\(C_p\)が大きいと、規格幅に対してばらつきが小さいことが分かりました。
しかし、たとえ\(C_p\)が1.33以上で特性のばらつきが小さくても、特性の分布の平均が規格中心から大きくずれていたら、規格から外れる可能性があります。
また、片側規格の場合は規格幅を求められません。
| 分布の平均と規格の中心がずれている場合 | 規格が片側のみの場合(上限規格の例) |
|---|---|
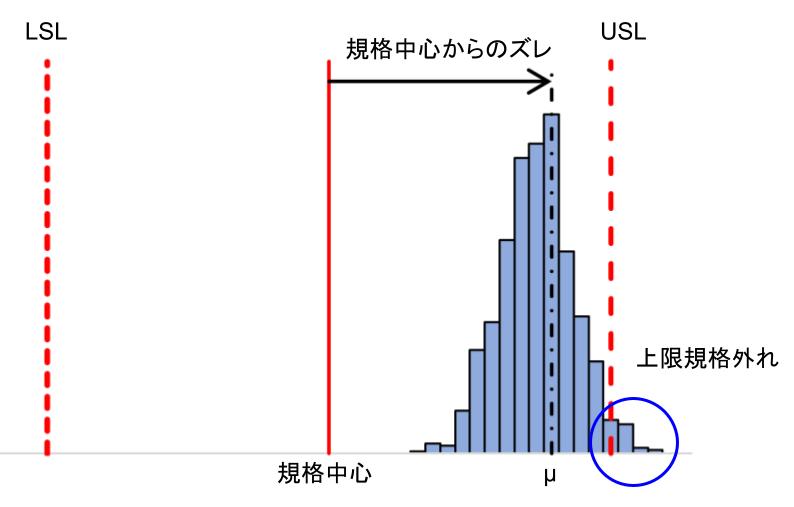 | 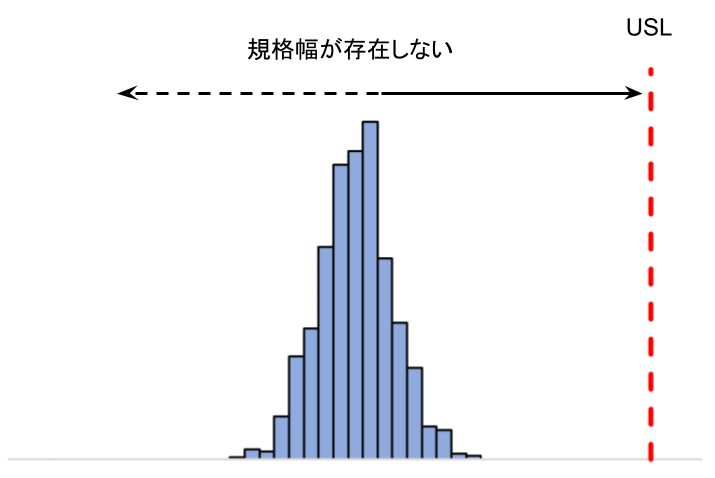 |
| 規格幅に対してばらつきは十分に小さいが、平均が規格の中心から上側に大きくずれているため、規格外れ品が生じている。 | 下限規格が存在しないため、規格幅を求められない。 |
このような場合に工程能力を評価する有効な指標が、「分布の平均と規格値との差」と「ばらつき\((3\sigma)\)」の大きさを比較した工程能力指数\(C_{pk}\)です。
2-4. 工程能力指数\(C_{pk}\)の計算方法と工程能力の評価
工程能力指数\(C_{pk}\)は、以下のように算出します。
| 片側規格(下限規格) | 片側規格(上限規格) | 両側規格 |
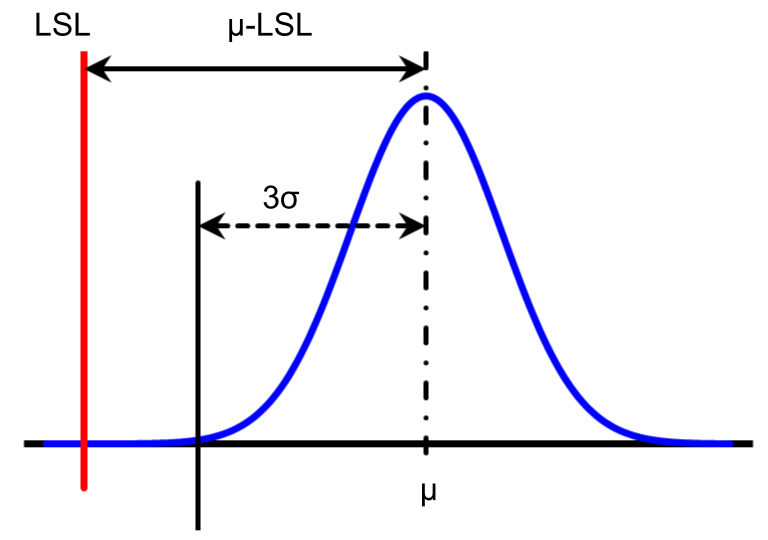 | 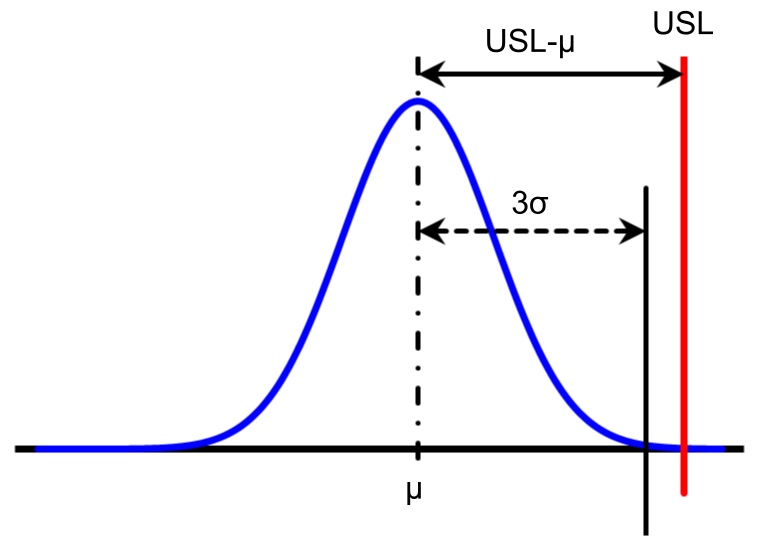 | 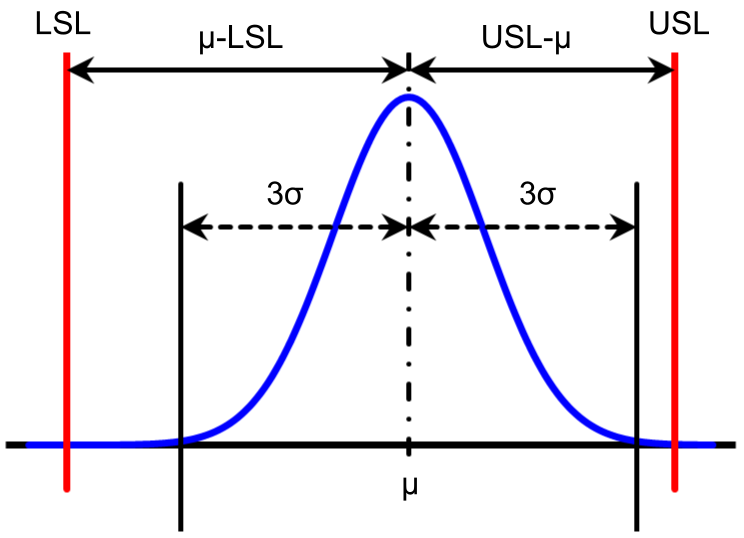 |
| $$C_{pkL}=\frac{\mu – LSL}{3\sigma}$$ | $$C_{pkU}=\frac{USL -\mu }{3\sigma}$$ | $$C_{pk}=min\{C_{pkL}, C_{pkU}\}$$ |
なお、\(min\{C_{pkL}, C_{pkU}\}\)とは、下側と上側それぞれについて\(C_{pkL}, C_{pkU}\)を計算して、小さい方の値を採用することを意味します。
得られた\(C_{pk}\)の値により、工程能力を以下のように判断します。
なお、\(C_p\)と同じく判断基準はルール化されているわけではないので、あくまで目安と考えてください。
| \(C_{pk}\)の値 | 工程能力の評価 |
|---|---|
| \(1.33\le C_{pk}\) | 規格に対して余裕があり、工程能力は十分ある状態 |
| \(1.0\le C_{pk} \lt 1.33\) | 規格に対して余裕はあるものの、平均のずれやばらつきの増加に注意が必要な状態 |
| \(C_{pk} \lt 1.0\) | 規格に対して余裕がなく、工程能力は不足している状態 |
ある製品の特性の上限規格は\(USL=54\)、下限規格は\(LSL=30\)です。
特性のデータが十分にあり、母平均\(\mu=34\)、母標準偏差\(\sigma=2\)のとき、工程能力指数\(C_p\)と\(C_{pk}\)を求めて工程の状態を判断しましょう。
【解答例】
\(C_p\)は事例1で求めた通り、\(C_p=2.0\)です。
$$C_{pk}=min \left \{\frac{34-30}{3\times 2},\frac{54-34}{3\times 2} \right \}=min \{0.67,3.33 \}=0.67$$
\(C_p\)は十分なものの、\(C_{pk}\)が1.0を下回っていることから、ばらつきは小さいものの分布の平均が規格中心からずれているために、工程能力が不足していると判断できます。
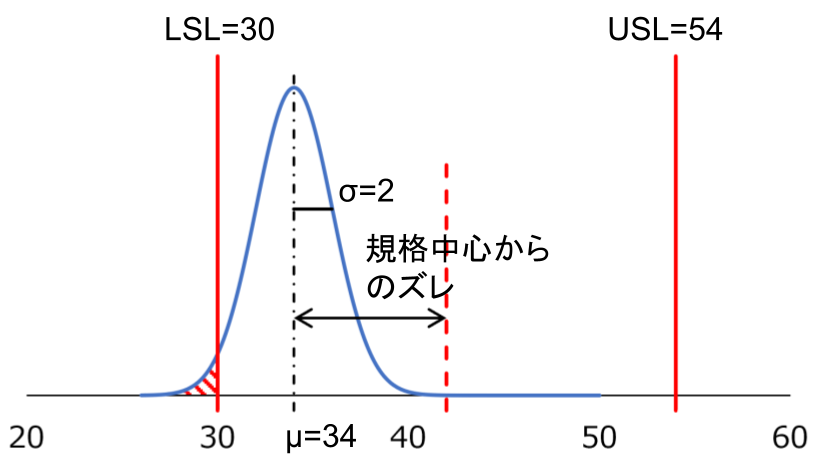
このような場合、分布の平均を規格の中心側に移す改善が求められます。
3. 工程能力指数\(C_{pk}\)と不良率の関係
これまで、工程能力指数の求め方や値の大小で工程能力の有無を判断できることを見てきました。
そもそも、なぜ工程能力指数を計算するのでしょうか?工程能力を把握する目的は何でしょうか?
それは、そのプロセスにおける不良率を簡単な計算で見積もれるからです。
工程能力がないということは、規格外れのリスクが高くつまり、不良率は高いことが推測できます。
工程能力が十分であれば、規格外れのリスクは低く不良率は小さいことが推測できます。
さて、正規分布を仮定できる場合、平均と標準偏差が分かれば積分により不良率を推定できることは、以前の記事で述べました。
 正規分布の活用方法を徹底解説
正規分布の活用方法を徹底解説
ただ、不良率を計算するのは大変なので(今は、Excelがあれば簡単に計算できますが)、簡単な計算でおおよその不良率を推定できる指標つまり、工程能力指数\(C_{pk}\)が求められるのです。
正規分布を前提としたときの\(C_{pk}\)と不良率の関係(両側規格の場合)
| 母平均\(\mu\)と規格との差 | \(C_{pk}\)の値 | 不良率の最大値(%) |
|---|---|---|
| 1\(\sigma\) | 0.33 | 31.73 |
| 2\(\sigma\) | 0.67 | 4.55 |
| 3\(\sigma\) | 1.00 | 0.27 |
| 4\(\sigma\) | 1.33 | 0.0063 |
\(C_{pk}\)から正確な不良率は求まりませんが、不良率の最大値(最悪値)を見積もれます。
一般的に目標とする\(C_{pk}=1.33\)を実現できれば、不良率は最悪でも0.0063%(63ppm)でほぼ不良品は発生しないと言えます。
4. 工程能力指数を求めるときの注意事項
最後に、工程能力指数を求めるときは、以下に注意する必要があります。
1) データが正規分布に従っていること
2) 十分なデータ数があること
1)については、正規分布を前提に、工程能力指数から不良率を推定します。
データが正規分布に従っていないと、工程能力は十分あるのに、不良品が発生するといったことが起こり得ます。
工程能力指数を計算する前に、まずはデータをヒストグラムで見える化し、正規分布に近いかを確認しましょう。
2)について、これまで工程能力指数を算出する際に、母平均\(\mu\)や母標準偏差\(\sigma\)を使ってきました。
これは、母集団つまり十分なデータ数で求めた平均値と標準偏差を用いる必要があることを意味します。
少ないデータでも工程能力指数は計算できますが、母集団の姿を正しく把握できない恐れがあるので、十分なデータ数(できれば100個以上、少なくとも30個以上)を確保してから、工程能力を算出してください。
どうしても十分なデータ数を確保できない場合は、工程能力指数の信頼区間を求めるという方法がありますが、これは別の記事で解説しています。
 サンプルサイズが小さいときの工程能力指数の推定
サンプルサイズが小さいときの工程能力指数の推定
5. 実践のためのアドバイス
工程能力指数は、平均と標準偏差が分かると計算できてしまうので、サンプル数が3で計算して工程能力は十分あると言う設計者がいますが、勘弁してほしいですね。
量産工程の工程能力を見極めるには、それなりのサンプル数が必要です。
設計段階では、無理に工程能力を推定するのではなく、規格の中心を狙って図面を作り込むことに注力するとよいでしょう。
6. おわりに
今回は、製造業でよく議論される、工程能力と工程能力指数について解説しました。
工程能力指数は簡単に計算でき、当該工程の不良率を容易に把握できるメリットがあります。
しかし、工程能力を正確に把握するには、正規分布に従う十分な数のデータで計算する必要があるので、注意してください。








