正規分布の活用方法を徹底解説

データ(計量値)を統計的に解析する上で、非常に重要な要素の一つが正規分布です。
データを集めると統計的な議論が可能となりますが、統計的な議論はデータが正規分布に従っていることを前提としています。

今回は、各種統計的手法の前提となる正規分布を解説します。

この記事で分かること

・正規分布とは何か
・正規分布における確率の計算方法
・標準正規分布表の使い方

1.　正規分布とは
2.　正規分布に基づく確率の求め方
- 2-1.　Excelを使った確率の求め方
- 2-2.　正規分布表を使った確率の求め方
3.　実践のためのアドバイス
4.　おわりに

1.　正規分布とは

ある製品の製造工程を考えてみましょう。
そこであなたは、製品の長さを測定しています。
得られる測定値はいつも同じでしょうか？決してそのようなことはないはずです。

どんなにばらつきをなくそうと厳しく管理しても、得られる測定値は必ずばらつきます。
十分な数の測定値を集めてヒストグラムを作ると、計量値であれば左右対称のヒストグラムを得られるのが一般的です。
そのヒストグラムを掘り下げてみましょう。

1-1.　サンプルを増やしたときのヒストグラム

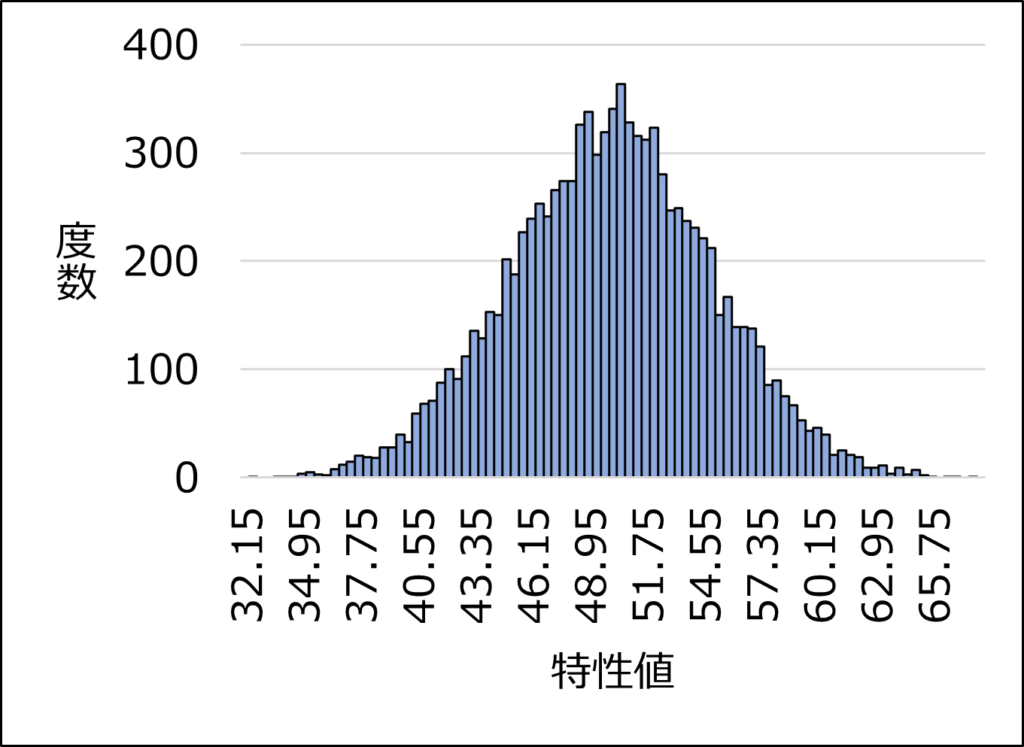
ある製品を製造している工程について、ある特性が母平均50、母標準偏差5で安定しているとしましょう。
この母集団から50個サンプリングしたときと、10000個サンプリングしたときでヒストグラムを作成すると、以下のようになります。(一つの例です。)

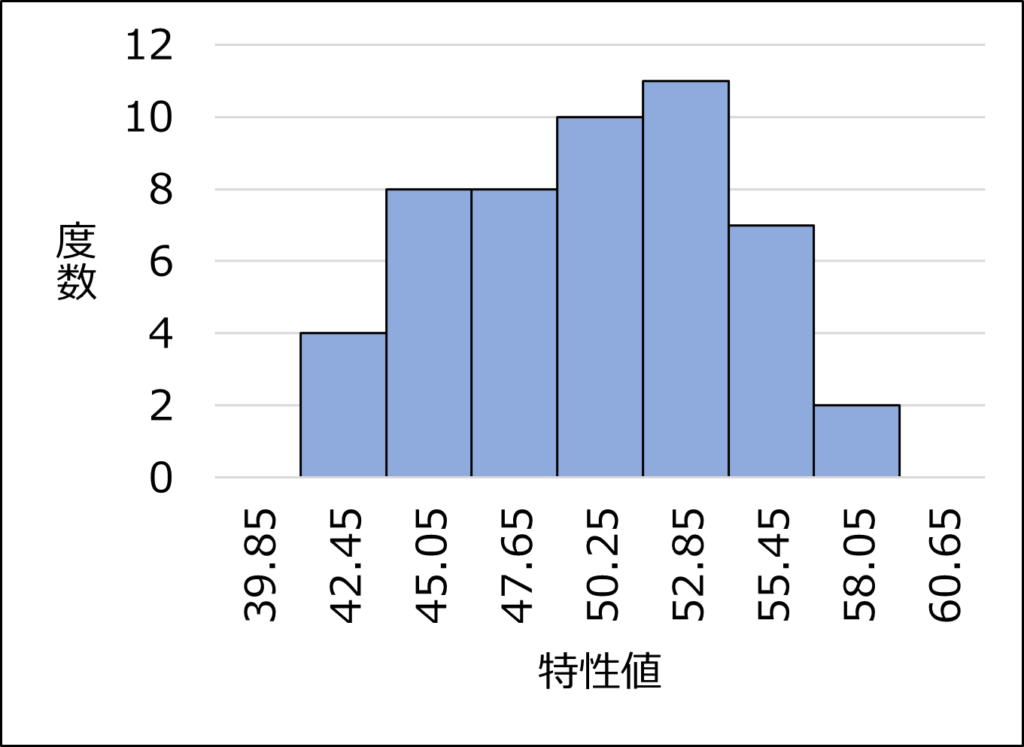
N=50では、区間の数は少ない(=区間の幅が広い)ですが、何となく左右対称に見えます。
それに対して、N=10000では、区間の数が増え(=区間の幅が狭い)、多少の凹凸はあるものの、左右対称の釣鐘状の形状であることが見て取れます。

このようにサンプルの数を増やしていくと、区間の幅が狭くなり、区間の数は増えていきます。
これは、ヒストグラムを作成する際に仮の区間$c$を求めるとき、
$$c=\sqrt{n}$$
で求めることからも、お分かりいただけるでしょう。(詳しくは、以下の記事を参照ください。)

2023年7月2日ヒストグラムの作り方とその分析方法

ここで、各区間における度数の代わりに、度数を総データ数で割った相対度数を縦軸にしてヒストグラムを作成すると、以下のようになります。

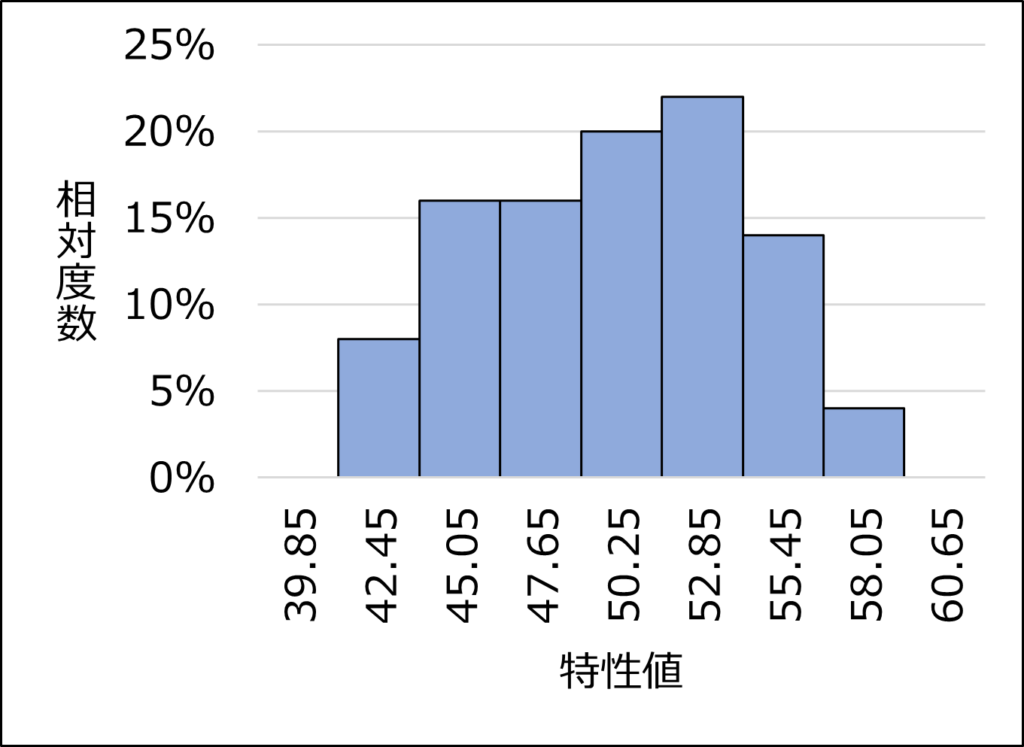
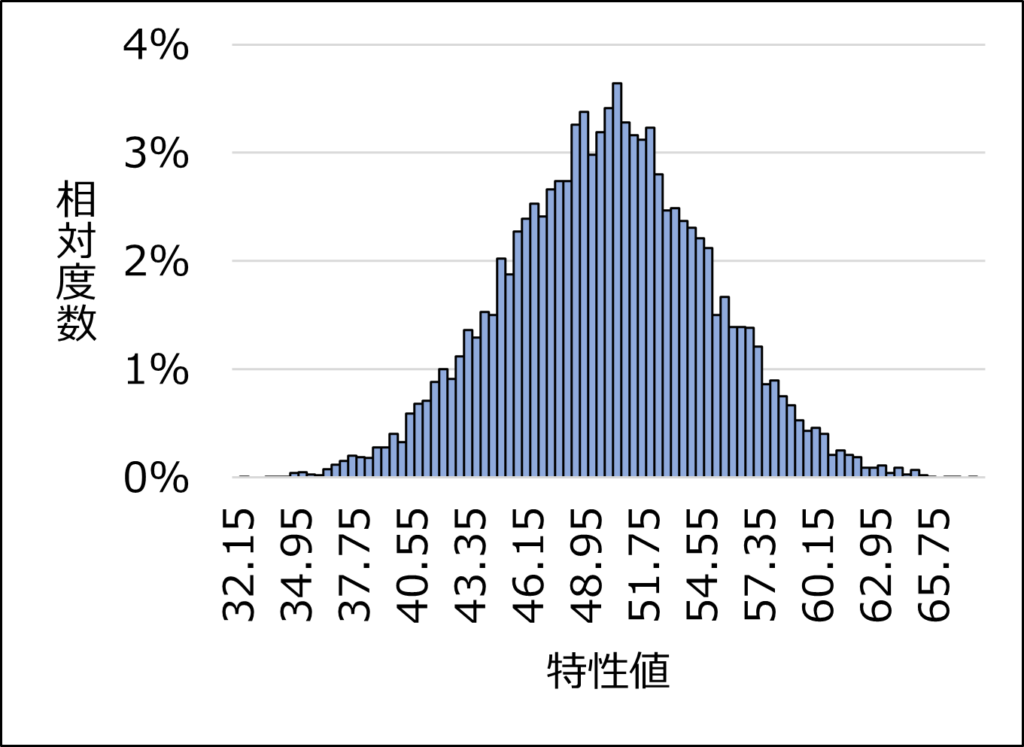
区間やヒストグラムの形状は変わりませんが、縦軸が相対度数になりヒストグラム全体の面積は1となります。

1-2.　正規分布とは

サンプリングする数をどんどん増やして母集団から、$n=\infty$個をサンプリング、つまり母集団のヒストグラムは、区間の数は無限となり形状は滑らかな曲線となります。
計量値の場合、左右対称の釣鐘状の分布になることが一般的で、このような分布を正規分布(ガウス分布)と言います。

例えば、母平均50、母標準偏差5の正規分布は、以下のようになります。

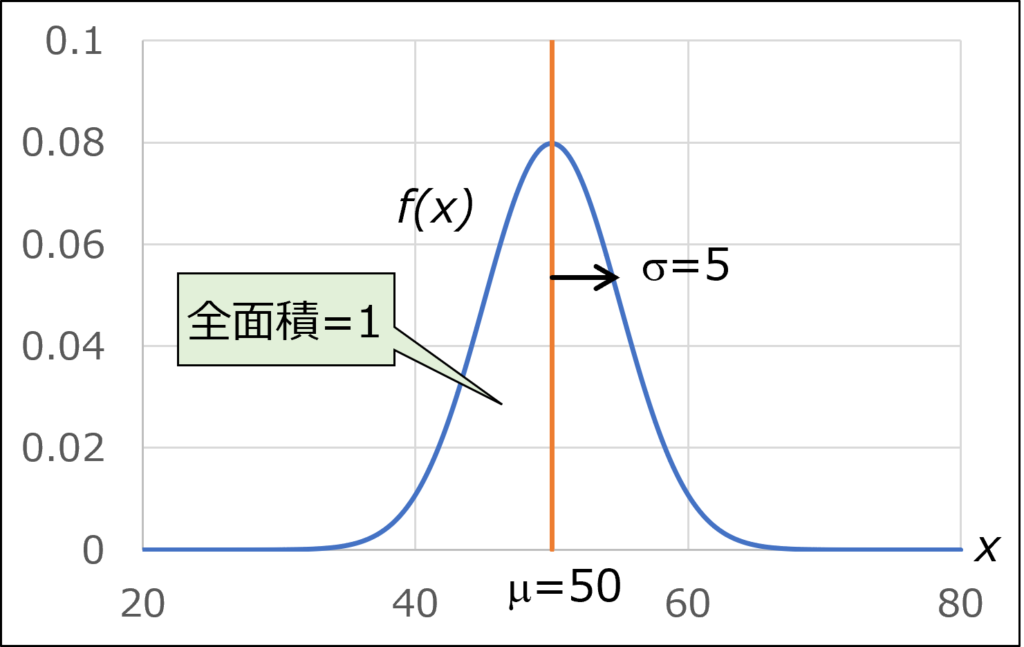
正規分布を表す関数$f(x)$のことを、正規分布の確率密度関数と言い、以下の式で与えられます。
$$f(x)=\frac{1}{\sigma\sqrt{2\pi}}exp\left \{-\frac{(x-\mu)^2}{2\sigma^2}\right \},\quad -\infty<x<\infty$$
正規分布の形状は、母平均$\mu$と母標準偏差$\sigma$(母分散$\sigma^2$)で決まります。
そこで、母平均$\mu$、母標準偏差$\sigma$の正規分布を$N(\mu, \sigma^2)$と表します。

また、曲線とx軸に囲まれた部分の面積は1となります。
したがって、正規分布の確率密度関数$f(x)$があるとき、$x$が区間$[a,b]$の範囲にある確率$P$は、以下のように確率密度関数の面積(積分)で求めることができます。
$$P=\int_a^{b}f(x)dx$$

1-3.　正規分布の形状と標準正規分布

前項で、正規分布は母平均$\mu$と母標準偏差$\sigma$で形状が決まると述べました。
母平均と母標準偏差を変化させると、正規分布$N(\mu,\sigma^2)$の形状は以下のように変化します。

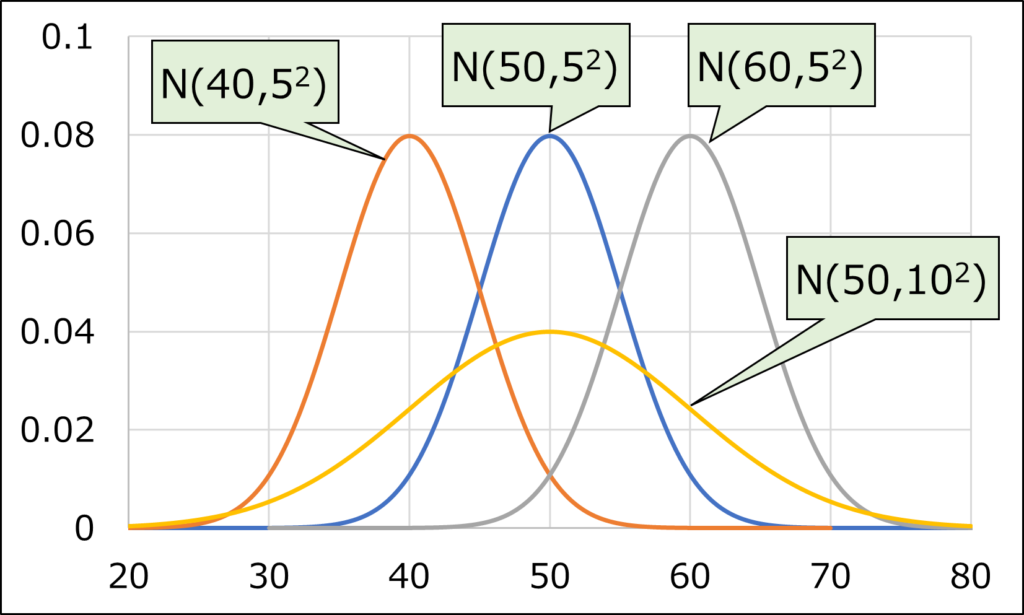
母平均が変化すると、正規分布の山の位置が横方向に変化します。
母標準偏差が変化すると、正規分布の山の幅が変化し、母標準偏差が大きくなるほど山の高さは低くなり、山の幅は広くなります。
これは、曲線とx軸に囲まれた部分の面積は1になる、という制約条件があるからです。

このように、母平均と母標準偏差の組み合わせによって、正規分布の形状は無限に存在しますが、特に母平均0、標準偏差1の正規分布$N(0,1^2)$を標準正規分布と呼びます。

2.　正規分布に基づく確率の求め方

計量値は正規分布に従うことが一般的ですが、正規分布に従うと仮定できると確率を計算できるというメリットがあります。
確率が計算できれば、不良率の推定や購買行動の予測など、ビジネスのさまざまな場面でものごとを統計的に判断することができます。
そこで、以下の事例を使って、正規分布を仮定できるときの確率の求め方を解説します。

【事例1】

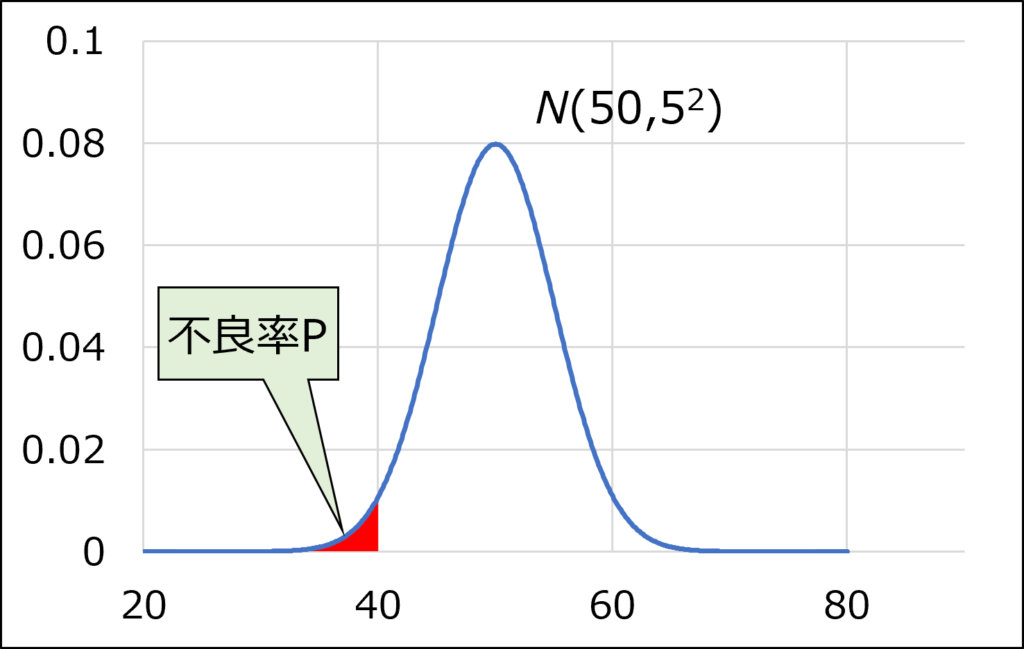
【事例】
ある製品の特性は過去の実績より、母平均50、母標準偏差5の正規分布に従うことが分かっています。
特性の規格が40以上のとき、この製品の不良率$P$を推定してみましょう。

2-1.　Excelを使った確率の求め方

正規分布で確率を求めたいときは、面積を求めればよかったですね。
全体の面積が1なので、赤い部分の面積を求めれば、それがそのまま発生確率(この場合は不良率)になります。
面積を求めるには、正規分布の確率密度関数を積分する必要がありますが、Excelには、NORM.DIST関数という正規分布の確率を計算できる関数があるので、この関数を使えば簡単に求まります。

任意のセルに、以下のように入力してください。
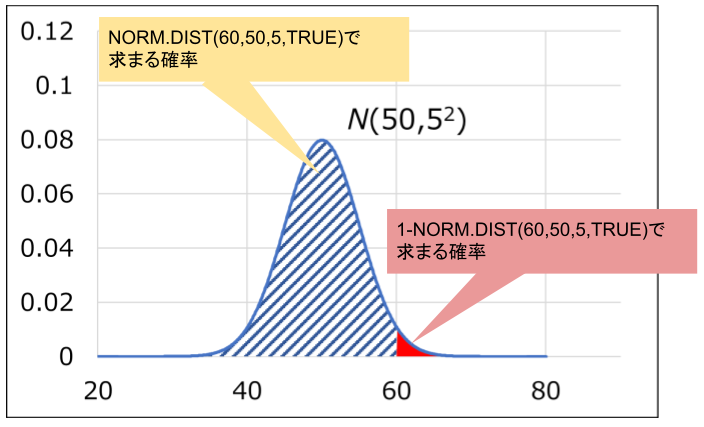
=NORM.DIST(40,50,5,TRUE)

するとセルには、0.02275(2.28%)と確率が表示され、これが不良率に該当します。
NORM.DIST関数は、指定した数値の左側の確率を計算してくれます。

もし、上の事例で規格が60以下という場合、単純にNORM.DIST関数を使うと合格率を計算してしまうことになるので、注意が必要です。
この場合は、正規分布全体の確率が1であることを利用して、1-NORM.DIST(60,50,5,TRUE)とすれば規格60を越える不良率を計算できます。

2-2.　正規分布表を使った確率の求め方

Excelを使うと正規分布における確率を簡単に求められますが、統計の書籍では正規分布表を使った求め方が紹介されています。
個人的には、パソコンがなかった頃の前近代的な求め方が必要なのかとは思いますが、統計検定や品質管理検定などを受検される場合は、正規分布表を使った確率の求め方を理解していなければなりません。
そこで、あまり実践的ではありませんが、正規分布表を使った確率の求め方も解説します。

手順1.　母平均$\mu$、母標準偏差$\sigma$、着目する数値$X$を把握する。

今回の場合は、母平均$\mu$は50、母標準偏差$\sigma$は5、着目する数値$X$は40です。

手順2.　$X$を標準化する。

正規分布の形状は、母平均$\mu$と母標準偏差$\sigma$の組み合わせによって無限に存在します。
そこで、$X$が標準正規分布$N(0,1^2)$上のどこに相当するのか、を求めます。
この作業を標準化(または、規準化/規準化)と言います。

これから使用する正規分布表は、標準正規分布における確率を列挙した表のため、正規分布表を使うためには標準正規分布に変換する必要があるのです。
$X$を標準化した値を$U$とすると、$U$は以下の式で求まります。
$$U=\frac{X-\mu}{\sigma}$$

事例の$X$を標準化すると、
$$U=\frac{40-50}{5}=-2$$
これは、$N(50,5^2)$の正規分布における$X=40$は、$N(0,1^2)$では$U=-2$に相当することを意味します。

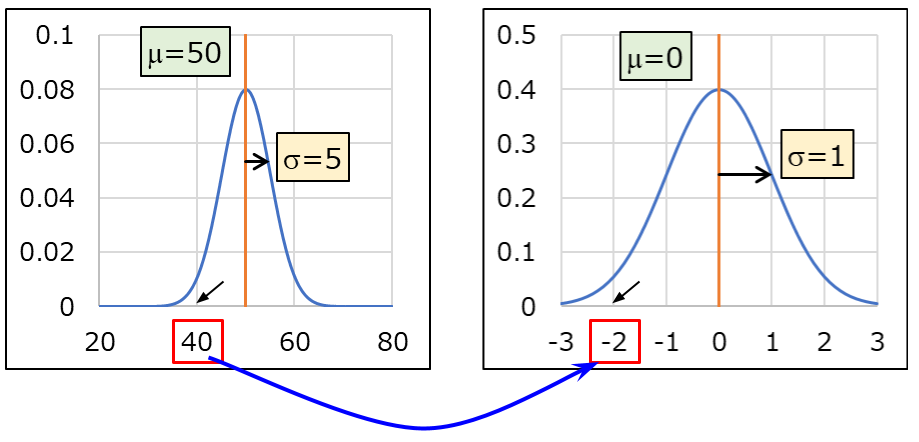
標準正規分布では標準偏差は1なので、$U$は平均から標準偏差の何倍離れているかを表しています。
なお、$U$の符号が$\textbf{＋}$であれば母平均から大きい方に、$\textbf{ー}$であれば母平均から小さい方に離れていることを指します。

手順3.　正規分布表から$U$に該当する確率を求める。

正規分布表とは、以下のような表です。

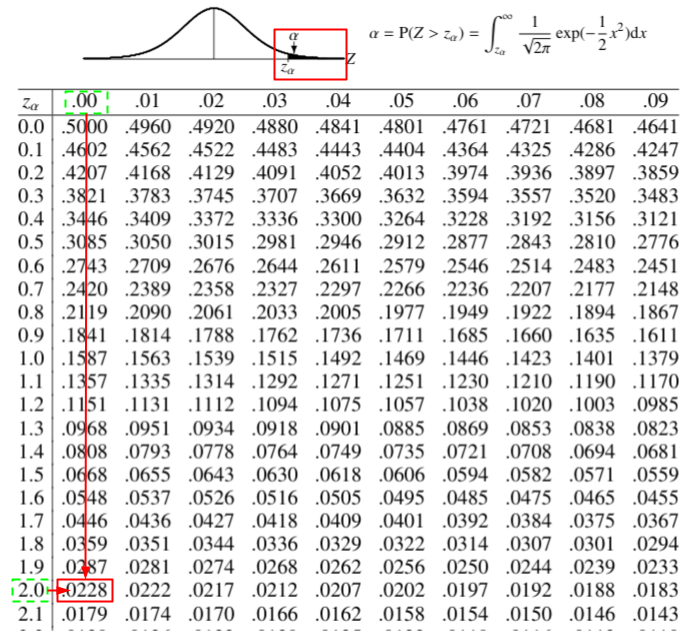
行方向が$U$の小数点第1位まで、列方向が小数点第2位の値です。

事例では$U=-2.00$で、正規分布は左右対称ですからーの符号を無視して、確率は2.28%であることが読み取れます。
(上の正規分布表では$z_\alpha$と記載)
なお、この確率が$U$の外側の確率を意味していることは、表の上の正規分布の$\alpha$の着色部で確認してください。