これまで、計量値の管理図である\(\bar{X}-R\)管理図と\(X-R_m\)管理図の作り方を解説しました。
工程改善のためには計量値に着目する機会が多いですが、JIS Z9020-2によると品質問題の80%以上は本質的には質的なものであるとのことです。
よって、計数値を対象とした管理図を作りたいというニーズもあり、計数値で工程を管理するために\(np\)管理図、\(p\)管理図、\(c\)管理図、\(u\)管理図が用意されています。
今回の記事では、\(np\)管理図の作り方を解説します。
1. 計数値管理図の特徴
計量値管理図では、通常は平均や個々のデータなど値の大きさを示す管理図と、ばらつきを管理するための管理図をペアで用います。
これは、計量値管理図は正規分布を仮定しているためで、正規分布は母平均と母分散という2つのパラメータで決まるため、ペアで用いることが必要ということです。
一方、計数値管理図は正規分布ではなく二項分布(\(np\)管理図、\(p\)管理図)、または、ポアソン分布(\(c\)管理図、\(u\)管理図)を仮定しており、両分布は1つのパラメータしか存在しないため、1つの管理図を考えれば十分なのです。
計数値管理図のやっかいな点は、群の大きさが変わると管理限界が変化する場合があることです。
\(np\)管理図と\(c\)管理図は群の大きさが一定の場合に用いるため、算出した管理限界線をそのまま伸ばせばよいですが、\(p\)管理図と\(u\)管理図は群の大きさが一定でない場合があるため、群ごとに管理限界を計算する必要があります。
ただし、実務では毎回管理限界を計算するのは大変なので、群の大きさが著しく変化しないのであれば、群の大きさの平均値に基づく一定の管理限界を用いることができる、とされています(JIS Z9020-2)。
2. \(np\)管理図とは
\(np\)管理図は、大きさが一定(\(n\))の群(サンプル)の中に、不適合品(不良品)が何個あったかをプロットした管理図です。
各群の不適合品率(不良率)を\(p\)とすると、不適合品の個数は\(np\)で表せることから、\(np\)管理図と呼ばれています。
3. \(np\)管理図の作り方
手順1 データを取る
大きさが一定のサンプルを20~25群取り、各群に含まれる不適合品数(不良品数)\(np\)を調べます。
なお、サンプルの大きさは当該工程の不適合品率(不良率)を予測して、サンプル中に1~5個程度の不適合品が含まれるように決めます。
\(np=1 \sim 5\)より、\(n=\displaystyle \frac{1}{p} \sim \frac{5}{p}\)が導けます。
例えば、工程の不良率が\(p=0.01\)と予測できるとすると、必要なサンプル\(n\)は以下のように算出できます。
\(n=\displaystyle \frac{1}{0.01} \sim \frac{5}{0.01}=100 \sim 500\)
手順2 管理線を計算する
管理線として中心線(CL)、上方管理限界線(UCL)、下方管理限界線(LCL)を計算します。
| \(np\)管理図 | |
|---|---|
| CL | \(n \bar{p}=\displaystyle \frac{\sum np}{k}\) ただし、 \(np\):各群の不適合品数 \(\sum np\):不適合品数の合計 \(k\):群の数 |
| UCL | \(n \bar{p}+3 \sqrt{n \bar{p}(1-\bar{p})}\) ただし、 \(\bar{p}=\displaystyle \frac{\sum np}{\sum n}=\frac{\sum np}{kn}\) \(\sum n\):検査個数の合計 |
| LCL | \(n \bar{p}-3 \sqrt{n \bar{p}(1-\bar{p})}\) ※値がマイナスになる場合、LCLは考えない。 |
手順3 管理図に記入する
サンプルの不適合品(不良品)数を縦軸に、群の番号を横軸に目盛り、各群の不適合品数を打点します。
さらに、手順2で求めた中心線、UCL、LCLとサンプルサイズ\(n\)を数値とともに記入します。
通常、中心線は実線、UCLとLCLは破線を用います。
手順4 管理状態にあるかを判定する
4. \(np\)管理図の作成例
20群(ロットサイズ\(n=2000\))のデータの例を使って、\(np\)管理図を作成してみましょう。
手順1 データを取る
| No | 不適合品数 |
|---|---|
| 1 | 2 |
| 2 | 5 |
| 3 | 0 |
| 4 | 6 |
| 5 | 0 |
| 6 | 1 |
| 7 | 2 |
| 8 | 1 |
| 9 | 1 |
| 10 | 7 |
| 11 | 1 |
| 12 | 0 |
| 13 | 2 |
| 14 | 3 |
| 15 | 2 |
| 16 | 4 |
| 17 | 1 |
| 18 | 1 |
| 19 | 0 |
| 20 | 3 |
手順2 管理線の計算
| \(np\)管理図 | |
|---|---|
| CL | \(n \bar{p}=\displaystyle \frac{\sum np}{k}=\displaystyle \frac{42}{2}=2.1\) |
| UCL | \(n \bar{p}+3 \sqrt{n \bar{p}(1-\bar{p})}\) \(=2.10+3 \sqrt{2.10 \times (1-0.0011)}=6.4\) |
| LCL | \(n \bar{p}-3 \sqrt{n \bar{p}(1-\bar{p})}=-2.2\)⇒マイナスなので考えない |
手順3 管理図に記入
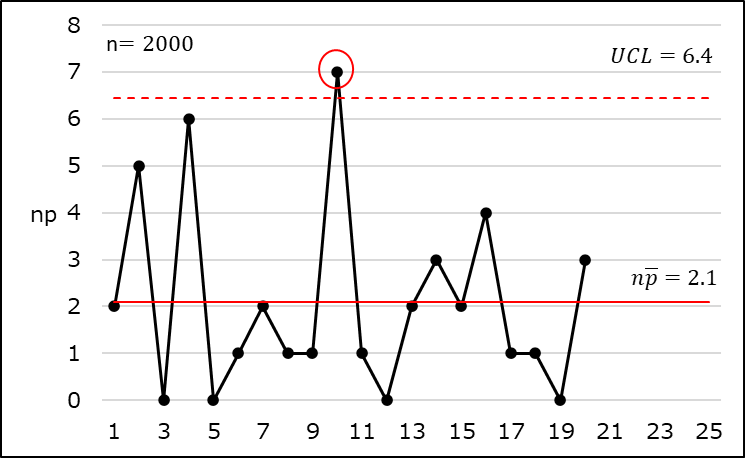
手順4 管理状態の判定
群番号10の打点がUCLを越えていることから、工程は管理状態にあるとは言えないと判定できます。
5. おわりに
今回は、\(np\)管理図の作り方を解説しました。
\(\bar{X}-R\)管理図や\(X-R_m\)管理図と違って、1つのグラフしか作らないことが理解できたと思います。
ただし、\(np\)管理図は検査結果が判明してからの管理図なので、不適合品が作られる前に異常を検知したいという目的であれば、プロセス内で得られる計量値の管理図で管理するとよいでしょう。