前回の記事で解説したように、管理図にはさまざまな種類がありますが、\(\bar{X}-R\)管理図は計量値で工程を解析したり管理したりする際に、最もよく使われる管理図です。
 工程管理における管理図の活用①~管理図とは
工程管理における管理図の活用①~管理図とは
\(\bar{X}-R\)管理図は工程平均の変化(群間変動)を見る\(\bar{X}\)管理図と、ロット内などのグループ内のばらつき(群内変動)を見る\(R\)管理図で構成されています。
2つの管理図をペアで使うことで、工程について多くの情報が得られるとても有用な管理図です。
今回の記事では、最も基本的な\(\bar{X}-R\)管理図の作り方を解説します。
1. 群内変動と群間変動
1-1. 群の設定
\(\bar{X}-R\)管理図では群の設定(群分け)をどうするか考える必要があります。
群分けには、工程の偶然原因による変化(群内変動)の大きさを求めることと、群の平均の変化(群間変動)を見ることの2つの目的があります。
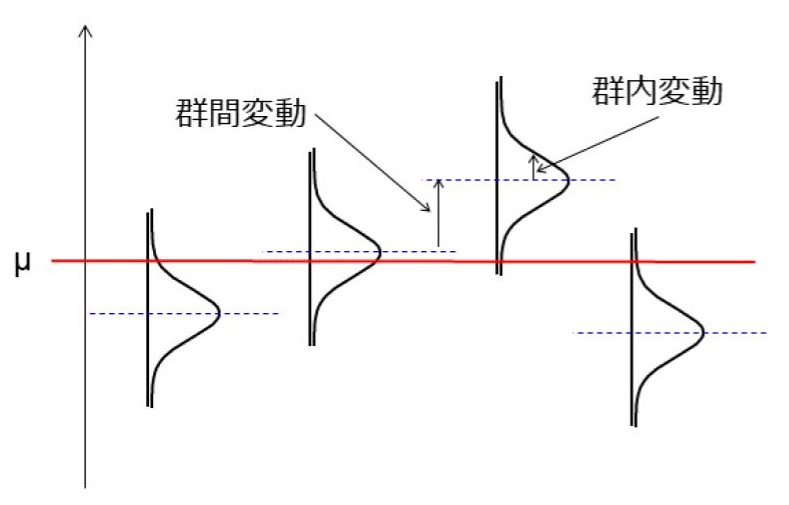
群内変動はR管理図で見ることができ、群内変動と群間変動を合わせた変動は\(\bar{X}\)管理図の\(\bar{X}\)のプロットのばらつきに現れます。
ここでポイントになるのが群分けです。
群の分け方によって、群内に含まれるばらつきの原因が変わってくるので、特に工程管理では何による変動を監視したいのか、を考えて群を決める必要があります。
生産直ごと、生産日ごと、材料ロットごと、製品ロットごとなど、操業上意味のある単位で群を考えるのが一般的ですが、群分けに困ったときは、以下のように考えてみてください。
(1)群内変動に効く原因と、群間変動に効く原因を、技術的に区別する。
(2)群内ではなるべく工程の状態が均一になるようにし、群内変動を偶然変動のみにする。
(3)特に管理したいばらつきが群間変動として現れるようにする。例えば、材料ロットが変わると特性も変わるのであれば、材料ロットごとに群を分ける。
群分けを必要以上に狭くすると経済的でなくなりますし、管理の手間を省くためにあまりに群分けを広くしすぎると、今度は異常を検出できなかったり、検出できたとしても処置が遅れたりします。
したがって、管理図を使った工程管理では、最初のステップである群分けがとても大切です。
1-2. サンプリング方法について
管理図では、群内変動=偶然変動となるように群分けすることが重要でした。
何が偶然変動であるかを技術的に考えることが求められますが、サンプリング方法やサンプルの処理方法、データ処理方法などが変わると、群内変動の意味が変わってくるので注意が必要です。
例として、量産している製品について、1日8時間の稼働で作られた製品を1つの群とし、そこから4個サンプリングして特性を測定するとします。
サンプリング方法として、以下の3パターンを考えます。
(1)連続4個をまとめてサンプリング
(2)2時間ごとにランダムに4個サンプリング
(3)4個をランダムにサンプリング
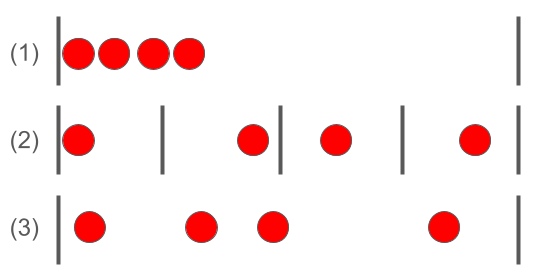
(1)~(3)はいずれも1日ごとに4個データが得られますが、同じn=4でも群内変動の意味が変わってきます。
この場合、特性のばらつきの大きさは「(1)の変動」\(\ll\)「(2)の変動」\(\le\)「(3)の変動」と考えられます。
(1)のサンプリング方法は、群内変動がかなり小さくなることが予想できます。
このようなサンプリングで\(\bar{X}-R\)管理図を作ると、\(R\)管理図は管理限界線内に収まるものの、\(\bar{X}\)管理図で管理限界線外れが多発し、使い物にならない管理図になることが多いです。
理想的なサンプリングは(3)のランダムサンプリングですが、サンプリング自体が難しい、経時変化をすぐにつかめないといった場合もよく起こります。
工程が2時間程度で大きく変動しないことが技術的に分かっているのであれば、(2)のサンプリング方法を1日を代表するサンプリングとみなしてもよいでしょう。
2. 標準値が与えられていない場合の\(\bar{X}-R\)管理図の作り方
\(\bar{X}-R\)管理図は工程から採取したサンプルについて測定した重量、寸法、製品強度などの計量値のデータについて、その\(\bar{X}\)と\(R\)を使って工程を管理する管理図で、工程管理でよく使われる代表的な管理図です。
\(\bar{X}-R\)管理図の作成手順を解説します。
手順1 データを取る
事前に決めた群ごとに大きさ4~5のデータを20~25群集め、合わせて約100個のデータにまとめます。
各群からあまりサンプルを取れないようであれば、群の数を増やします。
ただし、群を増やすことにより、製造条件が異なるデータや異質なデータが混入しないように気を付けてください。
また、群の大きさが一定でないと管理限界線の算出が複雑になるため、群の大きさは揃えましょう。
群の大きさ5で20群採取した以下の例を使って、管理図を作成します。
| 群の番号 | X1 | X2 | X3 | X4 | X5 |
|---|---|---|---|---|---|
| 1 | 174 | 154 | 164 | 162 | 166 |
| 2 | 168 | 166 | 164 | 164 | 170 |
| 3 | 170 | 166 | 164 | 162 | 166 |
| 4 | 162 | 165 | 153 | 167 | 165 |
| 5 | 162 | 160 | 160 | 168 | 166 |
| 6 | 175 | 167 | 165 | 169 | 159 |
| 7 | 166 | 168 | 174 | 166 | 160 |
| 8 | 158 | 172 | 168 | 162 | 164 |
| 9 | 164 | 162 | 160 | 170 | 148 |
| 10 | 151 | 159 | 153 | 165 | 147 |
| 11 | 164 | 166 | 164 | 164 | 170 |
| 12 | 164 | 162 | 163 | 158 | 163 |
| 13 | 158 | 162 | 168 | 154 | 172 |
| 14 | 164 | 156 | 162 | 158 | 152 |
| 15 | 162 | 164 | 152 | 156 | 164 |
| 16 | 174 | 156 | 162 | 162 | 174 |
| 17 | 181 | 168 | 151 | 158 | 154 |
| 18 | 172 | 166 | 162 | 166 | 164 |
| 19 | 160 | 166 | 170 | 170 | 160 |
| 20 | 168 | 160 | 160 | 154 | 162 |
手順2 群ごとに平均値\(\bar{X}\)を計算する
\(\bar{X}=\displaystyle \frac{X_1+X_2+\cdots+X_n}{n}\)
ただし、
\(X_1\):1番目の測定値
\(X_2\):2番目の測定値
\(\vdots\)
\(X_n\):n番目の測定値
\(n\):群の大きさ(各群のデータの数)
測定値の桁より2桁下まで計算し、最後の桁を四捨五入して測定値の1桁下まで求めます。
手順3 群ごとに範囲\(R\)を計算する
\(R=(X\)の最大値\()-(X\)の最小値\()\)
上記データについて、各群の平均値\(\bar{X}\)と範囲\(R\)を計算すると以下のようになります。
| 群の番号 | 平均値\(\bar{X}\) | 範囲\(R\) |
|---|---|---|
| 1 | 164.0 | 20 |
| 2 | 166.4 | 6 |
| 3 | 165.6 | 8 |
| 4 | 162.4 | 14 |
| 5 | 163.2 | 8 |
| 6 | 167.0 | 16 |
| 7 | 166.8 | 14 |
| 8 | 164.8 | 14 |
| 9 | 160.8 | 22 |
| 10 | 155.0 | 18 |
| 11 | 165.6 | 6 |
| 12 | 162.0 | 6 |
| 13 | 162.8 | 18 |
| 14 | 158.4 | 12 |
| 15 | 159.6 | 12 |
| 16 | 165.6 | 18 |
| 17 | 162.4 | 30 |
| 18 | 166.0 | 10 |
| 19 | 165.2 | 10 |
| 20 | 160.8 | 14 |
手順4 管理線を計算する
\(\bar{X}\)管理図と\(R\)管理図それぞれで、管理線として中心線(CL)、上方管理限界線(UCL)、下方管理限界線(LCL)を計算します。
| \(\bar{X}\)管理図 | \(R\)管理図 | |
|---|---|---|
| CL | \(\bar{\bar{X}}=\sum \bar{X}/k\) 測定値の桁より2桁下まで求める | \(\bar{R}=\sum R/k\) 測定値の桁より2桁下まで求める |
| UCL | \(\bar{\bar{X}}+A_2\bar{R}\) \(\bar{X}\)の桁より1桁下まで求める | \(D_4\bar{R}\) 測定値の桁より1桁下まで求める |
| LCL | \(\bar{\bar{X}}-A_2\bar{R}\) \(\bar{X}\)の桁より1桁下まで求める | \(D_3\bar{R}\) 測定値の桁より1桁下まで求める |
ただし、
\(k\):群の数
\(A_2, D_3, D_4\):群の大きさ\(n\)によって決まる数値(下表参照)
| サンプルの大きさ \(n\) | \(\bar{X}\)管理図 | \(R\)管理図 | |
| \(A_2\) | \(D_3\) | \(D_4\) | |
| 2 | 1.880 | 考えない | 3.267 |
| 3 | 1.023 | 考えない | 2.574 |
| 4 | 0.729 | 考えない | 2.282 |
| 5 | 0.577 | 考えない | 2.114 |
| 6 | 0.483 | 考えない | 2.004 |
| 7 | 0.419 | 0.076 | 1.924 |
| 8 | 0.373 | 0.136 | 1.864 |
| 9 | 0.337 | 0.184 | 1.816 |
| 10 | 0.308 | 0.223 | 1.777 |
事例のデータで管理線を求めると、以下のように求められます。
| \(\bar{X}\)管理図 | \(R\)管理図 | |
|---|---|---|
| CL | \(\bar{\bar{X}}=\sum \bar{X}/k\) \( =3264.4/20\) \(=163.22\) | \(\bar{R}=\sum R/k\) \(=276/20\) \(=13.80\) |
| UCL | \(\bar{\bar{X}}+A_2\bar{R}\) \(=136.22+0.577 \times 13.80\) \(=171.18\) | \(D_4\bar{R}\) \(=2.114 \times 13.80\) \(=29.1\) |
| LCL | \(\bar{\bar{X}}-A_2\bar{R}\) \(=136.22-0.577 \times 13.80\) \(=155.26\) | 考えない |
手順5 管理図に記入する
管理図は横軸を群番号とし、縦軸に\(\bar{X}\)管理図は\(\bar{X}\)を、\(R\)管理図は\(R\)としてデータをプロットします。
さらに、手順4で求めた中心線、UCL、LCLを数値とともに記入します。
通常、中心線は実線、UCLとLCLは破線を用います。
また、\(n\)の値を記入し、群の大きさが分かるようにします。
事例のデータについて、手順に従って管理図を作成すると、以下のようになります。
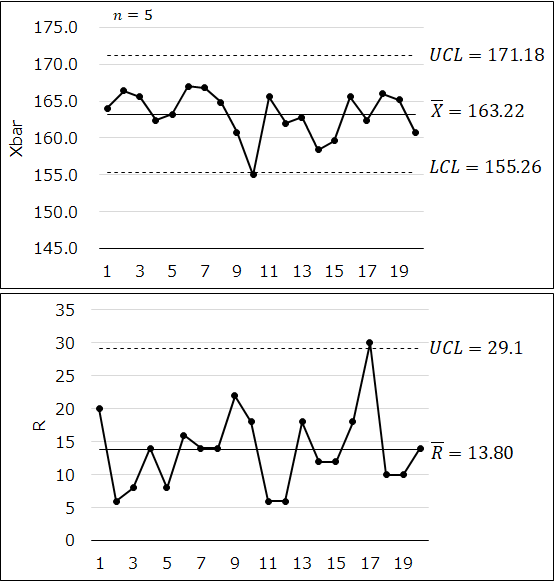
手順6 管理状態にあるかを判定する
以下の基本的な考え方にもとづいて、工程が管理状態にあるかどうかを判定します。
・点が管理限界線の外にでないこと
・店の並び方にくせがないこと
詳細な判定基準は別の記事で詳しく解説します。
事例の場合は、群10で\(\bar{X}\)がLCLを、群17で\(R\)がUCLを超えており、工程は管理状態にないと判断できます。
3. おわりに
今回は、\(\bar{X}-R\)管理図の作り方を解説しました。
その他の管理図も同じ手順で作成できるので、管理図を作成する際は本記事を参考にしてください。







