先の記事で、計量値は正規分布に従うことが多いことを解説しました。
正規分布とは、母平均を中心に左右対称の釣鐘状の分布のことでしたね。
 正規分布の活用方法を徹底解説
正規分布の活用方法を徹底解説
ところで、数値データは計量値以外にも、数えることで得られる計数値があります。
計数値はどのような分布に従うのでしょうか?
今回は、計数値が従う分布を解説します。
1. 計数値が従う分布とは
計数値とは、事故の件数、自動車の故障回数、不良品の数など数えて得られるデータでしたね。
計量値は正規分布に従いますが、計数値は一般的に正規分布ではなく、二項分布またはポアソン分布に従うことが知られています。
二項分布やポアソン分布は正規分布と全く関係がないというわけではなく、ある条件を満たすと正規分布に近似できるのです。
この特徴を利用して計数値の検定を行うのですが、検定については別の機会に解説します。
また、二項分布とポアソン分布にもお互い関係があります。
二項分布とポアソン分布を詳しく見ていきましょう。
2. 二項分布
まずは、二項分布について解説します。
二項分布はポアソン分布のベースになる分布なので、
2-1. 二項分布とは
不良品(不適合品)を\(P\)の割合(母不良率)だけ含む母集団から、\(n\)個の製品をランダムに選んだとき、そのうち\(x\)個が不良品である確率\(P(x)\)を考えます。
このとき、\(x\)は\(0,1,2,\cdots ,n\)の整数値を取ります。
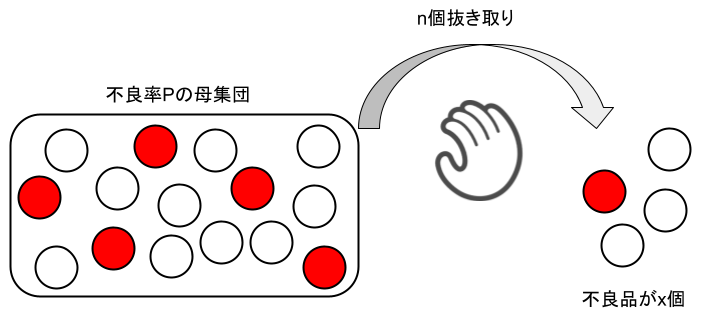
母不良率\(P=0.2\)の母集団から\(n=3\)個の製品を抜き取ったとき、3個の中に見つかる不良品の個数を\(x\)個とします。
このとき、\(x\)は\(0,1,2,3\)の値を取るので、それぞれの値を取る確率を計算してみましょう。
| \(n=3\)の組み合わせ | 確率 |
|---|---|
 | $$p_0=Pr(x=0)=(1-0.2)8^3=0.512$$ |
 | $$p_1=Pr(x=1)=3\times 0.2\times (1-0.2)^2=0.384$$ |
 | $$p_2=Pr(x=2)=3\times 0.2^2\times (1-0.2)=0.096$$ |
 | $$p_3=Pr(x=3)=0.2^3=0.008$$ |
表中の\(Pr(x)\)は、事象\(x\)が起こる確率を表します。
\(n=3\)個の組み合わせは表の組み合わせですべてなので、これらの確率をすべて加えると、1になります。
$$p_0+p_1+p_2+p_3=0.512+0.384+0.096+0.008=1$$
これを一般化すると、次のようになります。
$$p_r=Pr(x=r)={}_n C_kP^r(1-P)^{n-r}\quad (r=0,1,2,\cdots ,n)$$
$${}_n C_k=\frac{n!}{r!(n-r)!}$$
$$n!=n\times(n-1)\times\cdots\times3\times2\times1,\quad 0!=1$$
このような関数(確率関数)を持つ分布を二項分布と言います。
以前の記事で紹介した正規分布は、x軸は計量値で連続的な分布なので連続分布に分類されますが、二項分布のx軸は計数値で非連続な分布なので離散分布に分類されます。
2-2. 二項分布の形状
二項分布の形状は\(n\)と\(P\)で決まるので、二項分布は\(B(n,P)\)と表記します。
二項分布で\(n=20\)(一定)として、\(P\)の値を変化させて求めた分布と、\(P=0.1\)(一定)として、\(n\)の値を変化させて求めた分布を示します。
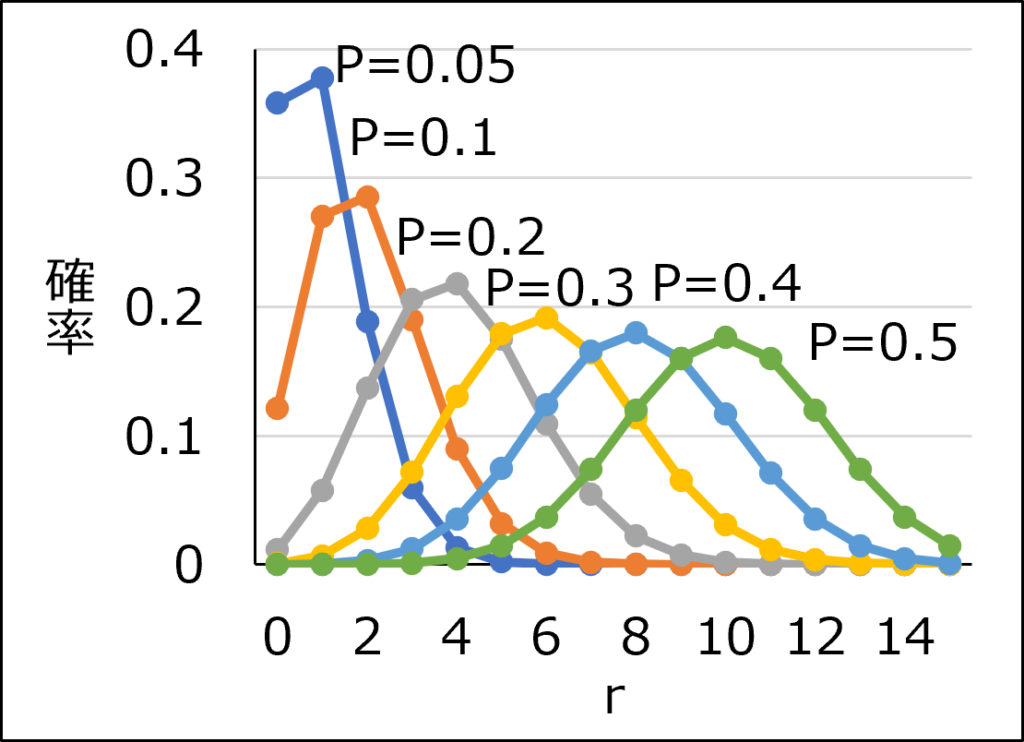
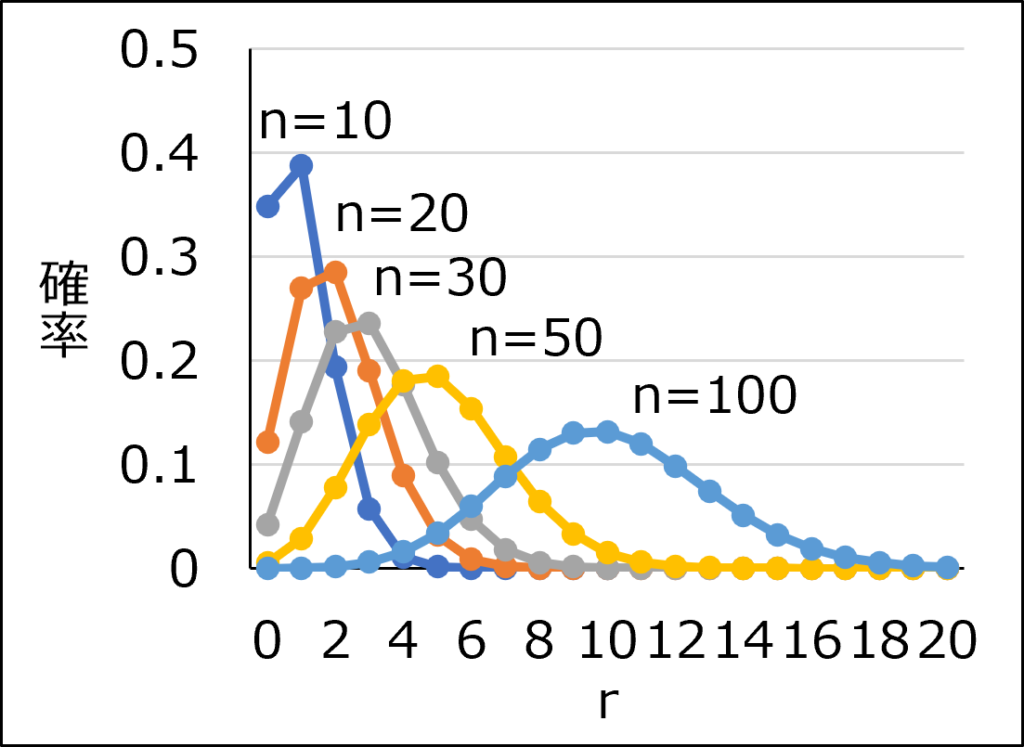
左のグラフから\(P\)が0.5に近づくほど、右のグラフから\(n\)が大きくなるほど、正規分布の形状に近づくことが分かります。
一般的には、\(nP\)および\(n(1-P)\)が5程度以上であれば、二項分布は正規分布に近似可能とされています。
正規分布に近似できるという特徴は、この後の検定で活用できます。
3. ポアソン分布
次に、ポアソン分布について解説します。
3-1. ポアソン分布とは
二項分布\(B(n,P)\)において、\(nP=\lambda\)と一定に保ち、\(n \to \infty,\quad P \to 0\)のときの分布をポアソン分布と言い、\(Po(\lambda)\)と表します。
このとき、\(\lambda\)を母欠点数(母不適合数)と呼びます。
二項分布を表す確率関数は、
$$pr=Pr(x=r)={}_n C_kP^r(1-P)^{n-r}$$
でしたが、\(nP=\lambda, n \to \infty,\quad P \to 0\)のとき、以下の確率関数を得ます。
$$pr=Pr(x=r)=\frac{\lambda ^r}{r!}e^{-\lambda} \quad (r=0, 1, 2, 3, \cdots)$$
二項分布で\(n \to \infty,\quad P \to 0\)ということは、抜き取る製品の個数\(n\)が非常に多く、母不良率\(P\)が非常に小さい場面を想定するということを意味します。
ある分布の極限を取ると得られる分布を極限分布と言いますので、ポアソン分布は二項分布の極限分布ということです。
3-2. ポアソン分布の形状
ポアソン分布は、二項分布の極限分布なので、両者の形状は似ていることが推測できます。
ポアソン分布は二項分布と同じく離散分布であり、\(nP=\lambda=5\)のとき、両者の形状を比較したものが以下のグラフです。
折れ線グラフが二項分布で、棒グラフがポアソン分布です。
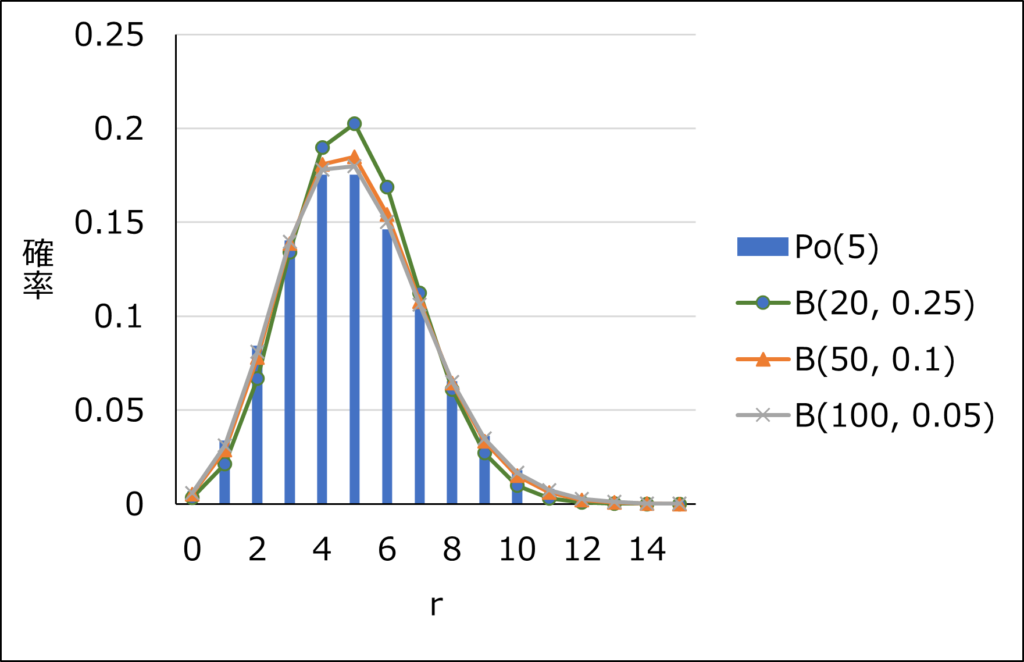
\(n\)が大きくなり、\(P\)が小さくなるほど、二項分布の確率はポアソン分布の確率に近づくことが分かります。
ポアソン分布について、\(\lambda\)の値を変化させたときの分布の違いを表したグラフが以下です。
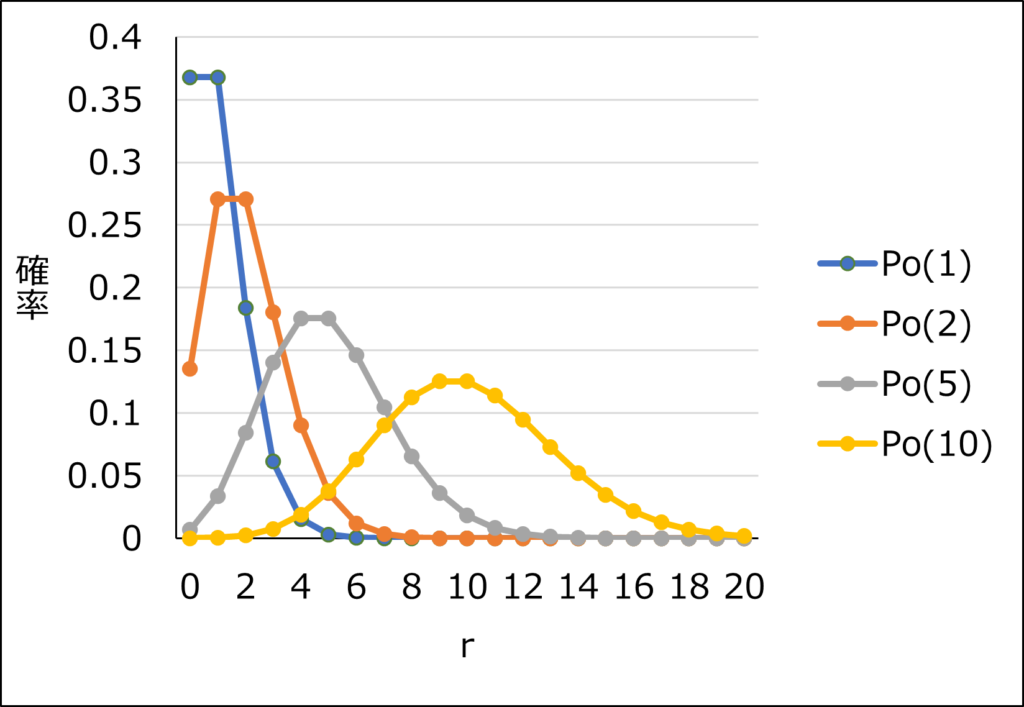
\(\lambda\)が大きくなるほど、ポアソン分布の確率関数は正規分布の確率密度関数に近づくことが分かります。
一般的には、\(\lambda\)が5以上であれば正規分布に近似できるとされています。
二項分布と同じく、正規分布に近似できるという特徴は検定で活かせます。
4. 実践のためのアドバイス
二項分布とポアソン分布は、計数値の解析においてお互い取り違えやすい分布です。
各サンプルが〇か×かを見るときは二項分布、サンプルの中の欠点を見るときはポアソン分布であることを覚えておきましょう。
5. おわりに
今回は、計数値の分布として代表的な二項分布とポアソン分布ついて解説しました。
計量値の分布である正規分布に比べると、計数値の分布を実務で使う機会は少ないですが、計数値の管理図、検定、抜取検査などで必要なので、計数値を使ったデータ解析をする方は二項分布とポアソン分布の違いをしっかり理解しておいてください。






