2つのデータの関係を確認するのに使われるグラフが「散布図」でした。
 散布図を使ったデータ解析方法
散布図を使ったデータ解析方法
散布図を見れば、2つの変数に関係があるかどうか、相関関係の有無を判断できます。
しかし、グラフの見た目で判断すると、人によって判断結果が異なることもあり得ます。
今回は相関関係の有無を定量的に判断できる、相関分析について解説します。
1. 相関分析とは
対になった2つのデータ\((x,y)\)が与えられているとき、\(x\)と\(y\)の関係を分析することを相関分析と言います。
相関分析を行うデータは、以下の2種類に分けられます。
1) \(x\)と\(y\)の因果関係ははっきりしていないが、関連の強さに関心がある場合。
例えば、勉強時間\((x)\)とテストの点数\((y)\)などです。
2) \(x\)が要因系で\(y\)が結果系のであることが明確な場合。
例えば、気温\((x)\)とアイスクリームの売上\((y)\)などです。
2. 相関係数とは
さて、相関分析を行う第一歩は散布図を描くことですが、2つのデータの関係の強さを数値で表す指標が相関係数\(r\)です。
相関係数\(r\)は\(-1≦r≦1\)の範囲を取り、\(r\)は正の相関が強いほど1に、負の相関が強いほど-1に近づき、相関関係がないと0に近くなる性質があります。
散布図と相関係数の例を以下に示します。
| 散布図 |  | 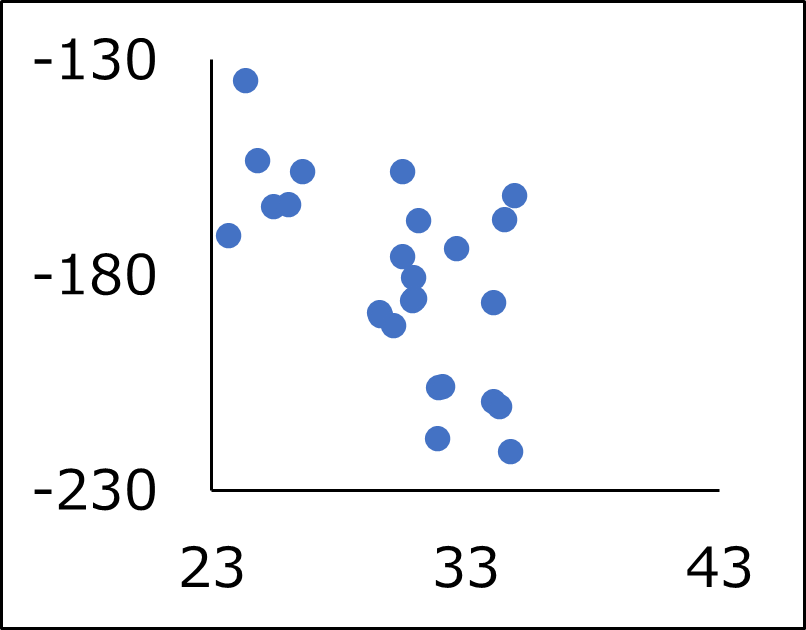 |  | 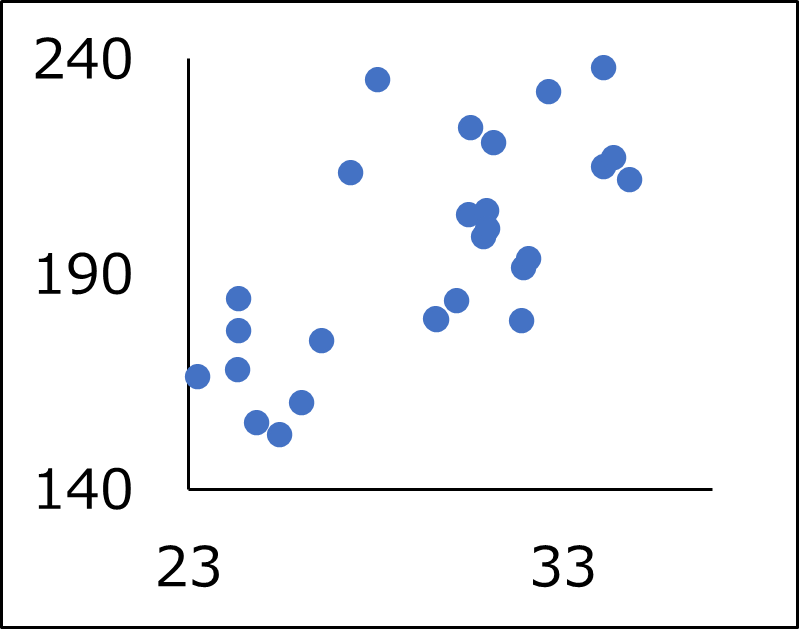 |  |
| 相関係数\(r\) | \(r=-0.98\) | \(r=-0.71\) | \(r=0.10\) | \(r=0.76\) | \(r=0.99\) |
両者の関係が直線に近づくほど、相関係数の絶対値は1に近づくことが分かります。
相関係数を求めれば、相関の強さを散布図の見た目だけでなく、数値で議論することが可能です。
3. 相関係数の求め方
相関係数は、Excelで簡単に計算できますが、どのような計算をしているのかを知りたい方のために、手計算の方法も示します。
以下のデータは、ある製品の長さと重量を測定したデータです。
| No. | 長さ(cm) | 重量(g) |
|---|---|---|
| 1 | 20.96 | 53.5 |
| 2 | 21.28 | 53.6 |
| 3 | 21.09 | 53.6 |
| 4 | 21.48 | 54.6 |
| 5 | 22.0 | 55.8 |
| 6 | 21.64 | 55.2 |
| 7 | 21.59 | 55.2 |
| 8 | 21.52 | 54.8 |
| 9 | 21.75 | 54.8 |
| 10 | 21.94 | 55.8 |
| 11 | 21.31 | 53.4 |
| 12 | 21.52 | 54.1 |
| 13 | 21.58 | 54.5 |
| 14 | 22.14 | 56.4 |
| 15 | 21.32 | 54.9 |
長さ\((x)\)と重量\((y)\)について散布図を作成すると、正の相関関係が見られます。
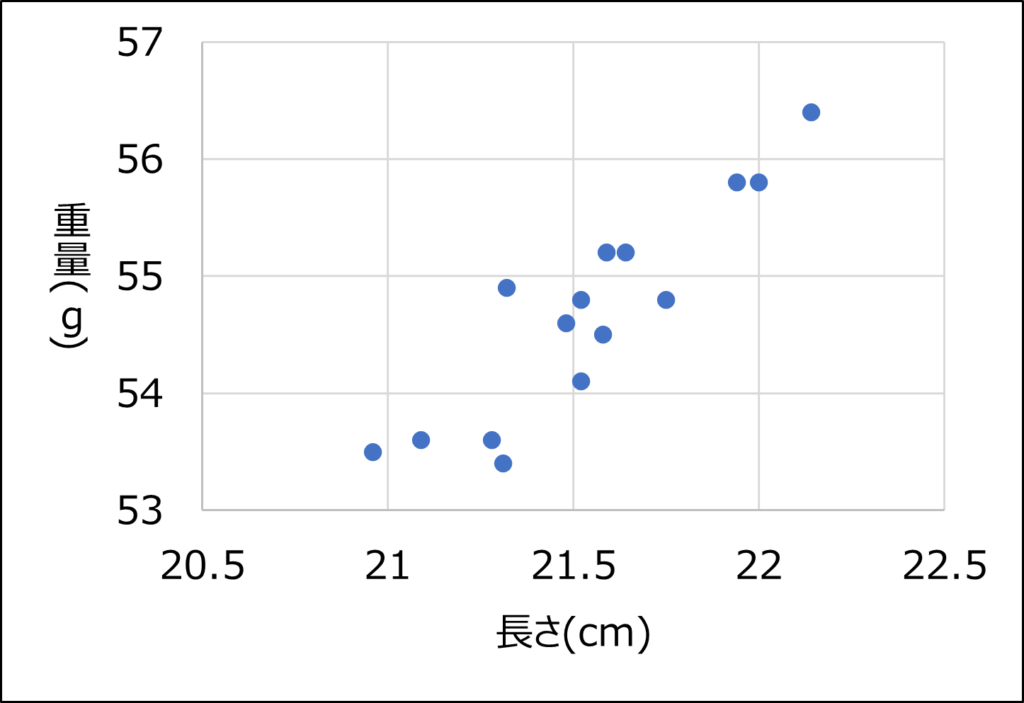
このデータについて、相関係数を求めてみましょう。
3-1. Excelを用いた相関係数の求め方
Microsoft Excelを使えば、簡単に相関係数を求められます。
Excelには「CORREL」という相関係数を計算してくれる関数があるので、この関数を用いると相関係数\(r=0.90\)が求まります。
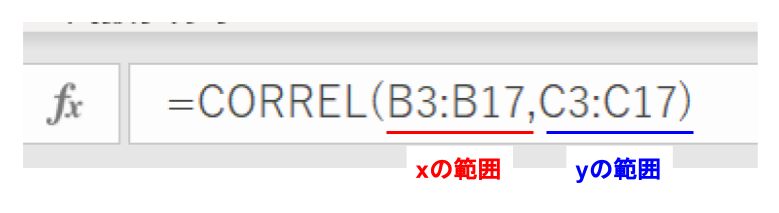
初めて使うときはアドインの操作が必要ですが、データ分析ツールにも「相関」のメニューがあり、こちらでも相関係数を求められます。
複数の変数同士の相関係数をまとめて見たい場合は、データ分析ツールを使うのが簡単です。
3-2. 手計算による相関係数の求め方
相関係数の導出過程を詳しく見ていきます。
相関係数\(r\)は以下の式で求めます。
相関係数:\(r=\displaystyle \frac{S_{xy}}{S_{xx}S_{yy}}=\frac{xとyの偏差積和}{\sqrt{(xの偏差平方和)(yの偏差平方和)}}\)
各項は、以下のように計算します。
\(x\)の偏差平方和:\(S_{xx}=\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})^2=\sum_{i=1}^{n}x_i^2-\frac{(\sum_{i=1}^{n}x_i)^2}{n}\)
\(=(xの個々のデータの2乗の合計)-\displaystyle \frac{(xの合計)^2}{データ数}\)
\(y\)の偏差平方和:\(S_{yy}=\displaystyle \sum_{i=1}^{n}(y_i-\bar{y})^2=\sum_{i=1}^{n}y_i^2-\frac{(\sum_{i=1}^{n}y_i)^2}{n}\)
\(=(yの個々のデータの2乗の合計)-\displaystyle \frac{(yの合計)^2}{データ数}\)
\(x\)と\(y\)の偏差積和:\(S_{xy}=\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})\)
\(=\displaystyle \sum_{i=1}^{n}x_iy_i-\displaystyle \frac{(\sum_{i=1}^{n}x_i)(\sum_{i=1}^{n}y_i)}{n}\)
\(=(xとyの積の合計)-\displaystyle \frac{(xの合計)(yの合計)}{データ数}\)
以上の式に事例のデータを代入すると、以下のようになります。
\(S_{xx}=(20.96^2+21.28^2+\cdots +21.32^2)-\displaystyle \frac{(20.96+21.28+\cdots +21.32)^2}{15}\)
\(=6961.94-\displaystyle \frac{(323.12)^2}{15}=1.502\)
\(S_{yy}=(53.5^2+53.6^2+\cdots +54.9^2)-\displaystyle \frac{(53.5+53.6+\cdots +54.9)^2}{15}\)
\(=44860.36-\displaystyle \frac{(820.2)^2}{15}=11.824\)
\(S_{xy}=(20.96\times53.5+21.28\times 53.6+\cdots +21.32\times 54.9)\)
\(-\displaystyle \frac{(20.96+\cdots +21.32)(53.5+\cdots +54.9)}{15}\)
\(=17672.00-\displaystyle \frac{323.12\times 820.2}{15}=3.8024\)
したがって、相関係数\(r\)は以下のようになります。
$$r=\displaystyle \frac{S_{xy}}{\sqrt{S_{xx}S_{yy}}}=\frac{3.8024}{\sqrt{1.502\times 11.824}}=0.902$$
得られた相関係数\(r\)の値は1に近いことから、長さ\((x)\)と重量\((y)\)の間には、強い正の相関あると言えます。
4. 実践のためのアドバイス
相関分析では、2つの変数の関係性を相関係数で定量化できます。
特に、要因系と結果系の散布図を作成し、相関係数が大きいと因果関係があると判断しがちですが、それは必ずしも正しいとは言えません。
因果関係があると相関係数は大きくなりますが、その逆は真とは限らないことに留意しましょう。
5. おわりに
今回は、相関分析について解説しました。
相関の強さは相関係数で表せ、その算出方法を理解いただけたと思います。
相関の強さを定量的に評価したいときは、相関係数を求めてましょう。
なお、相関分析を行うにあたっていくつか注意事項があるのですが、それは次の記事でまとめて解説します。
 2変数の関係を定量化する方法~相関分析②~
2変数の関係を定量化する方法~相関分析②~ 





