収集したデータを、属性や条件などについて共通点を持つグループに分けることを層別と言います。
層別は、問題のある場所や問題を引き起こす原因を見つけるのに、とても重要な考え方です。
今回は、層別の意義や重要性を解説します。
1. 層別とは
収集したデータをそのまま解析しても、特徴を見い出せなかったり、問題解決につながる結果を得られなかったりすることがよくあります。
そのようなときはデータを、年齢別、地域別、原材料別、作業別など、属性や条件などでデータを分割すると、特徴や傾向が見えることがあります。
これを層別と言います。
どのグループで分割すべきかは、分割してみないと分からないことも多いので、仮説を立ててその仮説に基づいて層別するのがおすすめです。
2. 層別の必要性
層別を行うとどんな効果があるのでしょうか?
ヒストグラムと散布図を例に、層別の必要性を見ていきます。
2-1. ヒストグラムにおける層別
以前ヒストグラムの記事で、二山型や高原形といった形状のヒストグラムを紹介しました。
このようなヒストグラムが得られたときは、データを層別すれば傾向が見えることがあります。
事例をもとに、層別の効果を見てみましょう。
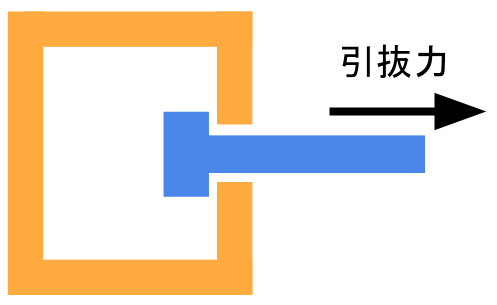
ある製品について、部品の引抜力を測定しています。
引抜力の規格は90N以上ですが、最近規格を下回る不良品が発生しており、問題解決が求められています。
現状把握のため、直近に製造した製品の引抜力のデータを収集し、ヒストグラムを作成しました。(N=200)
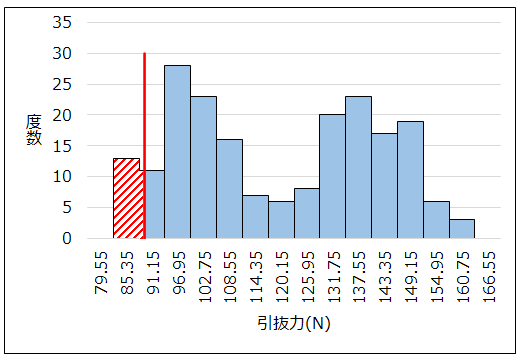
ヒストグラムを見ると、確かに規格外れが発生しています。
また、ヒストグラムは2山の形状をしており、2つの母集団からのサンプルが混ざっていることが推定できました。
当該製品は設備Aと設備Bで製造しているので、設備で層別してヒストグラムを作成しました。
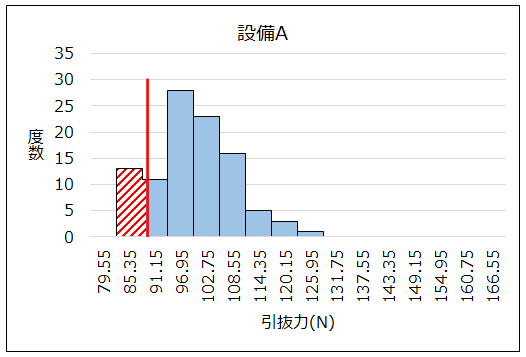
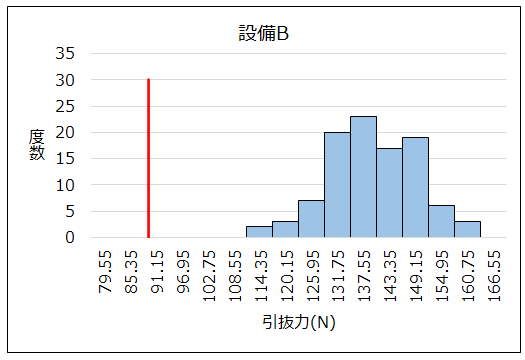
設備Bで作った製品の引抜力は、規格に対して十分に余裕があり、問題はないと判断できます。
それに対して、設備Aで作った製品は規格外れが発生しており、設備Aに何らかの問題が発生していると判断でき、設備Aについて要因解析を進めました。
このように、層別することにより、調査対象を設備Aに絞ることができました。
 ヒストグラムの作り方とその分析方法
ヒストグラムの作り方とその分析方法
2-2. 散布図における層別
散布図を作成すると、対になった2つのデータについて相関関係があるかを確認できます。
しかし、複数の母集団からのデータが混ざった状態で散布図を作成すると、本当は相関関係があるのに無相関に見えたり、逆に本当な無相関なのに相関関係があるように見えたりすることがあります。
このようなときは、データを層別することによって、正しい相関関係を把握できます。
Aさんは地域の運動会のリレーメンバーを組もうとしています。
候補者の年収と50m走のタイムを見ると、年収が少ないほどタイムが早い傾向があることが分かりました。
そこで、Aさんは「年収の少ない人を集めれば最強のチームが作れるぞ」と意気込んでいます。
疑問に感じたあなたは、Aさんが作った散布図を見せてもらいました。
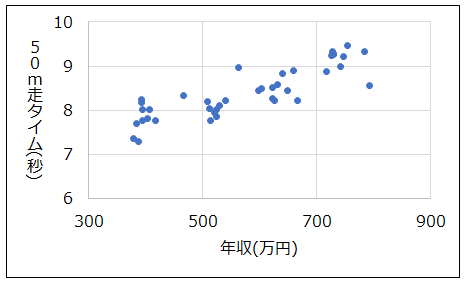

確かに、直線関係が見られますが、原理・原則から考えると、年収と50m走のタイムに相関関係があるとは思えません。
そこで、年代で層別してみました。
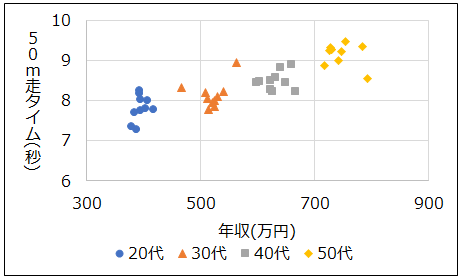
層別した結果を見ると若いほどタイムが速く、年齢が高くなるほど遅くなっており、若い方が体力的に勝ることを考えると、これは納得のいく結果です。
一方、同一年代内で見ると、年収とタイムに相関関係があるとは言えませんが、これも当然の結果ですね。
一般的に、年齢が高くなるほど年収も上がりますので、最初の散布図の年収は年齢を代用していたということです。
このように、相関があるように見えるデータも、層別すると無相関になることもありえますので、原理・原則を考えておかしいと思ったら層別を考えてください。
 散布図を使ったデータ解析方法
散布図を使ったデータ解析方法

3. 実践のためのアドバイス
問題解決においては、良い状態と悪い状態で差異を見つけることが重要であり、層別の考え方は必須です。
データを収集する前に、どのように層別すると違いが見えそうかの仮説を立ててかを想定して、仮説を検証するつもりでデータを収集しましょう。
4. おわりに
今回は、層別について解説しました。
グループごとに挙動が異なる場合は、データの層別が必須です。
問題解決において、効率的に真因を突き止めるためには、調査のポイントを絞り込むことが必要であり、層別は問題解決において非常に重要な考え方です。
マーケティングの世界でも、対象を層別して、それぞれのグループに適したアクションを取ることはよく行われます。
データを取ったらそのまま解析するだけでなく、必要に応じて層別して解析してみてください。