ヒストグラムの作り方とその分析方法

1.　ヒストグラムとは

ヒストグラムとは、データ(計量値)の各区間における出現頻度を度数表にまとめ、度数に比例した面積を持つ柱を並べた図です。

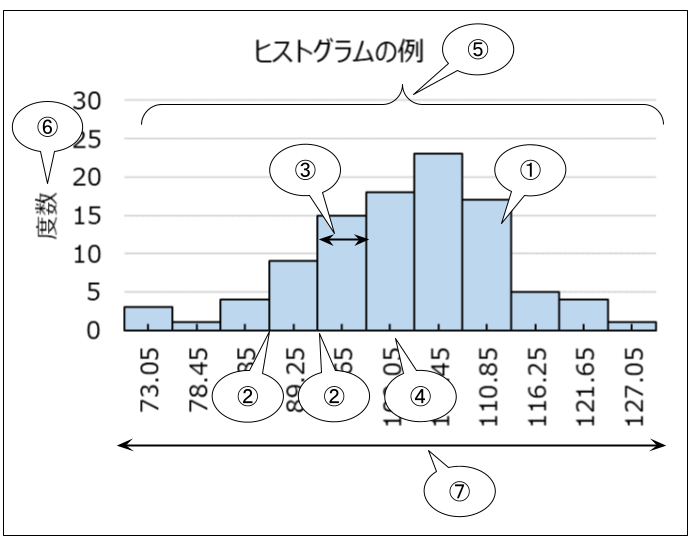
①　区間(級、クラスと言うこともある)
②　区間の境界値(上側 / 下側)
③　区間の幅\((h)\)
④　区間の中心値\((x)\)
⑤　区間の数
⑥　度数(\(f\)と表すこともある)
⑦　分布(データのばらつき度合い)

横軸が特性値、縦軸がデータの個数(度数)であり、ヒストグラムを作ると、分布の状態や形状の確認、データのばらつき度合い、規格値との比較、異常値の有無などを直感的に把握できます。

2.　ヒストグラムの作り方

Microsoft Excel(2016以降)には、グラフメニューの中にヒストグラムがあり、データがあれば簡単に作成できます。

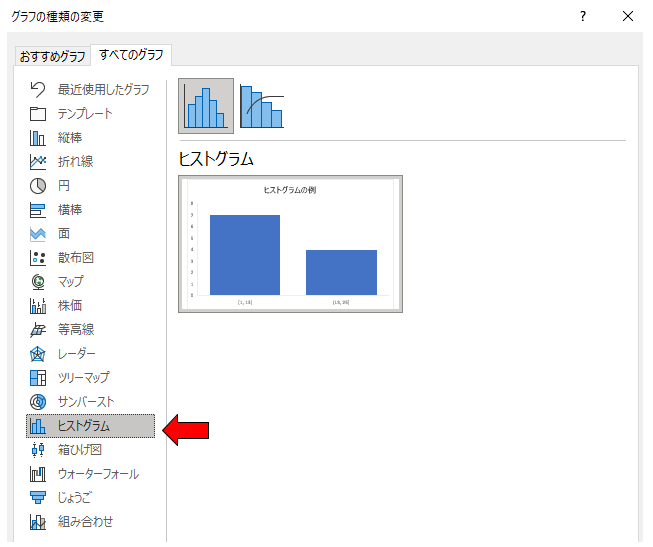
Excelのバージョンが2016より前であれば、度数表を作って棒グラフでヒストグラムを作ってください。

このようにヒストグラムはExcelで簡単に作れますが、区間の幅や区間の数などを丁寧に求めたいという方のために、品質管理の教科書に掲載されている伝統的な作り方を紹介します。
実際に数値があった方が分かりやすいので、ある運送業者に所属するトラックの走行距離を事例にしてヒストグラムを作ってみましょう。

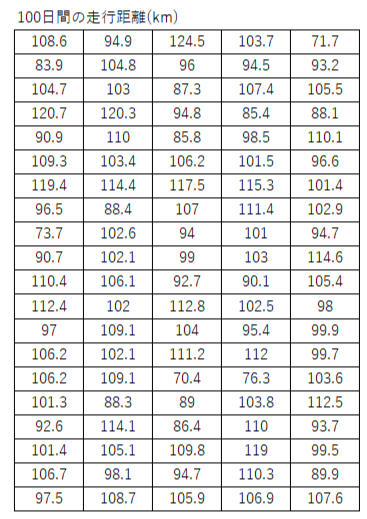
手順1.　目的とする特性を明確にし、データを収集する。

このとき、測定単位\((m)\)(測定の刻み)を把握しておく。
ばらつき度合いを見るには、100個程度のデータを集めることが望ましい。

事例では、測定単位は0.1kmで100個のデータがあります。

手順2.　データ数\((n)\)に対して、仮の区間\((c)\)を求める。
$$c=\sqrt n$$
事例では、\(c=\sqrt {100}=10\)となります。

手順3.　データの最大値\((x_{max})\)と最小値\((x_{min})\)を探して範囲\((R)\)を求め、区間の幅\((h)\)を決める。
なお、求めた区間の幅\((h)\)は、四捨五入して測定単位\((m)\)の桁に数字を丸める。
$$h = \frac{R}{c}=\frac{x_{max}-x_{min}}{c}$$
ヒストグラムに規格値を入れたい場合は、規格値を含めて区間の幅を計算する。

事例では、最大値は124.5、最小値は70.4なので、
$$h =\frac{124.5-70.4}{10}=5.4$$
となります。

手順4.　最初の第1区間の下側境界値を求める。

第1区間の下側境界値 \(=\) 最小値\(-\displaystyle \frac{測定単位}{2}=x_{min}-\frac{m}{2}\)
第1区間の上側境界値は、下側境界値に区間の幅\((h)\)を加える。
以降の区間については、下側境界値は前の区間の上限境界値とし、上側境界値は区間の幅\((h)\)を加えることを繰り返し、最大値を含む区間まで求める。

事例では、第1区間の境界値は以下のようになります。
第1区間の下側境界値\(=x_{min}-\displaystyle \frac{m}{2}=70.4-\frac{0.1}{2}=70.35\)
第1区間の上側境界値\(=70.35+5.4=75.75\)

手順5.　各区間の下側境界値と上側境界値から区間の中心値\(x\)を求める。

区間の中心値\(=\displaystyle \frac{上側境界値+下側境界値}{2}\)

事例の第1区間の中心値は、以下となります。
第1区間の中心値\(=\displaystyle \frac{75.75+70.35}{2}=73.05\)

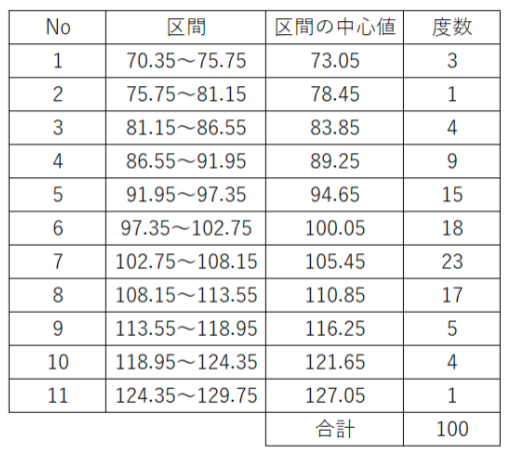
手順6.　各区間に入るデータを数え、各区間の度数\(f\)を求めて度数表を作成する。

事例の度数表は以下のようになります。
度数を求めるのに、一つずつ数えるのは大変なので、Excelのfrequency関数、countif関数、データ分析ツールなどを使うと、素早く正確に求められます。

手順7.　度数表をもとにヒストグラムを作成する。

事例のヒストグラムは以下のようになります。

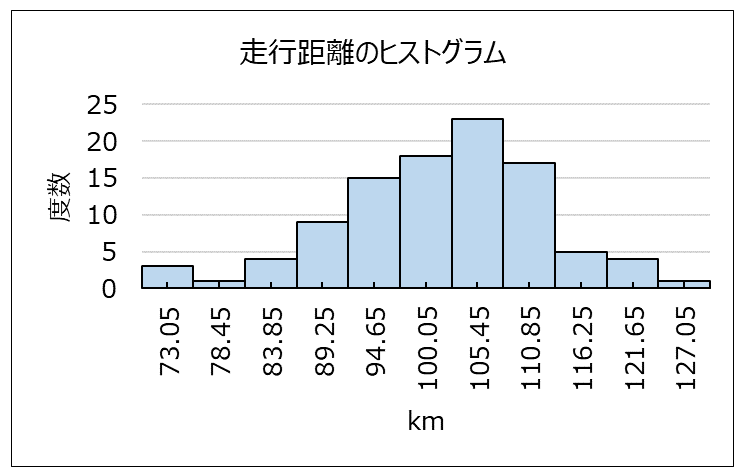
これで、ヒストグラムが完成です。

なお、ヒストグラムの作り方は一つではなく、例えばJIS Z 9041-1「データの統計的な解釈法ー第1部：データの統計的記述」では、区間の幅の決定方法は本稿と異なる方法が記載されていますので、気になる方はJISをご確認ください。

3.　ヒストグラムの見方

ヒストグラムでは、
1)　分布の状態や形状の確認、異常値の有無の確認
2)　データのばらつき度合い、規格値との比較
が可能です。
1)と2)について、ヒストグラムとの関係を詳しく解説します。

3-1.　分布の形状

分布の形状を見るときは、多少の凹凸は気にせず、分布全体に着目しましょう。
通常の計量値データであれば、ヒストグラムの中央付近が最も高く、左右に離れるほど山が低くなる左右対称の釣り鐘状になることが多いです。
ヒストグラムのパターンと特徴を示します。

ヒストグラムの形と名称	特徴
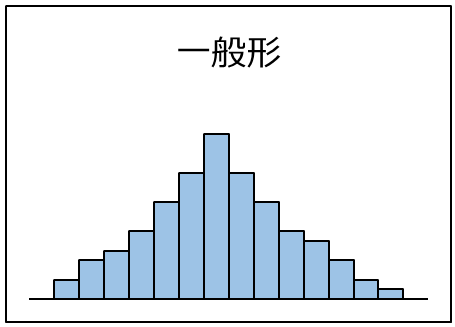	一般形。 通常現れる形で、左右対称の釣り鐘のような形状。 平均値は山の中央付近に存在する。
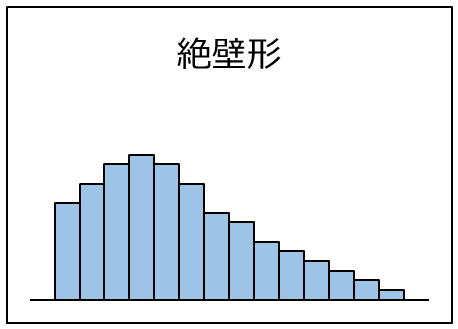	絶壁形。 一般形の左端または右端が切れている形状。 規格外のサンプルを除いて作成した場合に見られる。
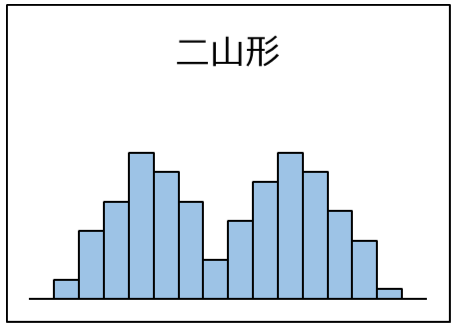	二山形。 平均値の異なる２つの母集団のデータが存在する状態。 例えば、2台の機械で作った製品のデータが混ざっているなど。 層別してヒストグラムを作成するとよい。
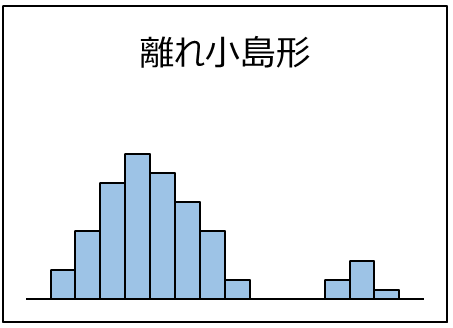	離れ小島形。 異品の混入や工程の異常などの異常がある場合に見られる。 データを確認して原因追究するとよい。
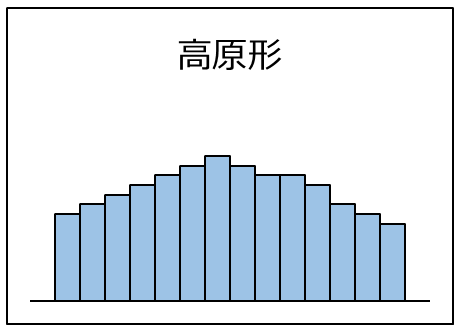	高原形。 平均値の異なる複数の分布が重なり合っている状態。 層別してヒストグラムを作成するとよい。
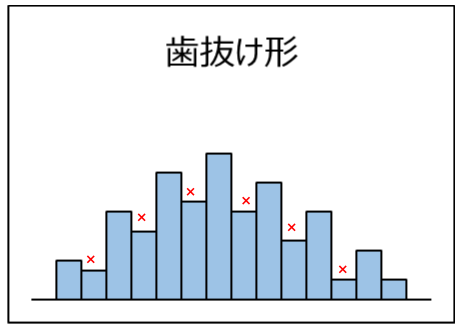	歯抜け形。 測定方法がまずかったり、区間の幅の決め方がまずかったりするときに見られる。

3-2.　規格値との比較

ヒストグラムに上限規格\((S_U)\)と下限規格\((S_L)\)を入れると、規格に対して十分に余裕があるかを見ることができます。

ヒストグラムと規格の関係	特徴
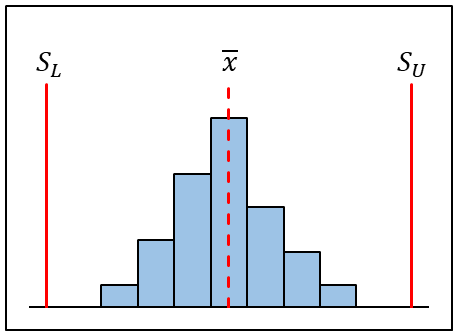	規格幅に対してばらつきは小さく、平均値も規格のほぼ中央にあり理想的な状態。
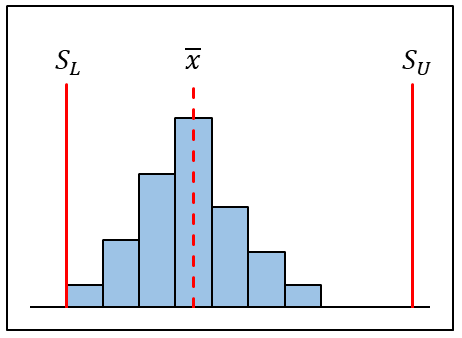	規格幅に対してばらつきは小さいものの、平均値が規格の中央からずれており、平均値がさらにずれたら規格を外れる状態。 平均値を規格の中央に移す処置が必要。
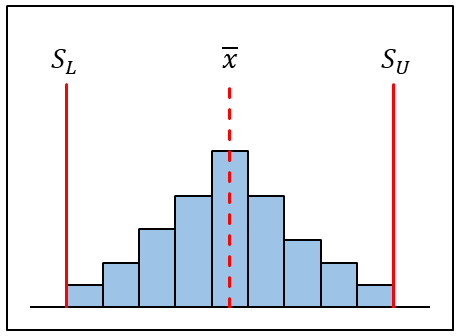	平均値は規格中央にあるものの、規格幅に対してばらつきが大きく、少しでも平均値がずれたら規格を外れる状態。 ばらつきを小さくする処置が必要。
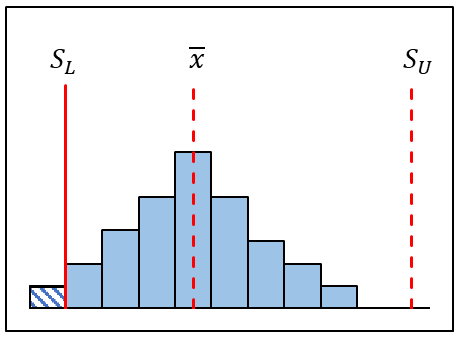	規格幅に対してばらつきが大きく、平均も規格の中央からずれているため規格外れが発生している状態。 平均値を規格の中央に移す処置と、ばらつきを小さくする処置が必要。
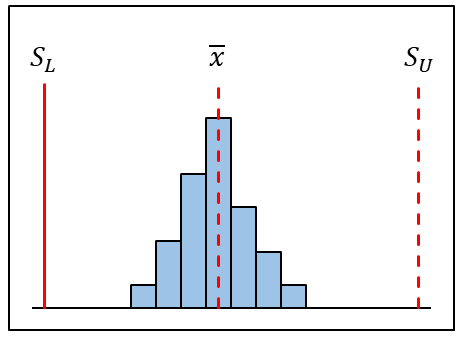	規格幅に対してばらつきが非常に小さく、規格外れの心配はほとんどない。 ただし、ばらつきを抑えるためにコストなどをかけているのであれば、それを見直す検討をしてもよい。

4.　実践のためのアドバイス

データ解析のための手法の中には、解析対象のデータが正規分布に従っていることを前提としたものがあります。
正規分布しているかどうかを確認する最も簡便な方法の一つが、ヒストグラムを描くことです。
ヒストグラムを見れば多くの情報が得られるので、データ解析においては重要なツールです。
実務では境界を厳密に決めなくても目的は達成できるので、Excelでパッと作成するとよいでしょう。

5.　おわりに

今回は、ヒストグラムについて解説しました。

ヒストグラムを作成すると、分布の状態や規格値との関係がひと目で分かります。
工程の管理状態を見るときだけでなく、データ解析する際も解析の前にまずはヒストグラムを作成し、採取したデータの分布を把握するようにしてください。