計数値の管理図として、不適合品数を管理する\(np\)管理図と不適合品率を管理する\(p\)管理図の作り方を解説しました。
いずれの管理図も、対象はサンプルが合格か不合格かを調査した結果をプロットするもので、二項分布に従うことを利用して管理限界を算出しました。
計数値が従う分布としてもう一つ有名なのがポアソン分布で、ポアソン分布に従う不適合数(欠点数)を管理する管理図も存在します。
それが、\(c\)管理図と\(u\)管理図です。
今回の記事では、\(c\)管理図の作り方を解説します。
1. \(c\)管理図とは
\(c\)管理図は、不適合(欠点)の現れる範囲の大きさが一定の製品や工程を不適合品数(欠点数)で管理する場合に用います。
例えば、一定面積のガラス板のキズの数、一定の長さのホースの気泡の数などで工程を管理する場合です。
2. \(c\)管理図の作り方
手順1 データを取る
大きさが一定のサンプルを20~25群取り、各群に含まれる不適合数(欠点数)\(c\)を調べます。
なお、サンプルの大きさは、サンプル中に1~5個程度の不適合が含まれるように決めます。
手順2 管理線を計算する
管理線として中心線(CL)、上方管理限界線(UCL)、下方管理限界線(LCL)を計算します。
| \(c\)管理図 | |
|---|---|
| CL | \(\bar{c}=\displaystyle \frac{\sum c}{k}\) \(\sum c\):不適合数の合計 \(k\):群の数 |
| UCL | \(\bar{c}+3 \sqrt{\bar{c}}\) |
| LCL | \(\bar{c}-3 \sqrt{\bar{c}}\) ※値がマイナスになる場合、LCLは考えない。 |
手順3 管理図に記入する
サンプルの不適合(欠点)数を縦軸に、群の番号を横軸に目盛り、各群の不適合品数を打点します。
さらに、手順2で求めた中心線、UCL、LCLを数値とともに記入します。
通常、中心線は実線、UCLとLCLは破線を用います。
手順4 管理状態にあるかを判定する
3. \(c\)管理図の作成例
20群のデータの例を使って、\(c\)管理図を作成してみましょう。
手順1~2
| No | 不適合数 |
|---|---|
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 1 |
| 6 | 2 |
| 7 | 3 |
| 8 | 1 |
| 9 | 4 |
| 10 | 3 |
| 11 | 0 |
| 12 | 2 |
| 13 | 1 |
| 14 | 2 |
| 15 | 6 |
| 16 | 1 |
| 17 | 0 |
| 18 | 2 |
| 19 | 0 |
| 20 | 1 |
| 合計 | 31 |
手順5 管理線の計算
| \(c\)管理図 | |
|---|---|
| CL | \(\bar{c}=\displaystyle \frac{\sum c}{k}=\displaystyle \frac{31}{20}=1.6\) |
| UCL | \(\bar{c}+3 \sqrt{\bar{c}}=1.6+3 \sqrt{1.6}=5.4\) |
| LCL | \(\bar{c}-3 \sqrt{\bar{c}}=1.6-3 \sqrt{1.6}=-2.2\)⇒考えない |
手順4 管理図に記入
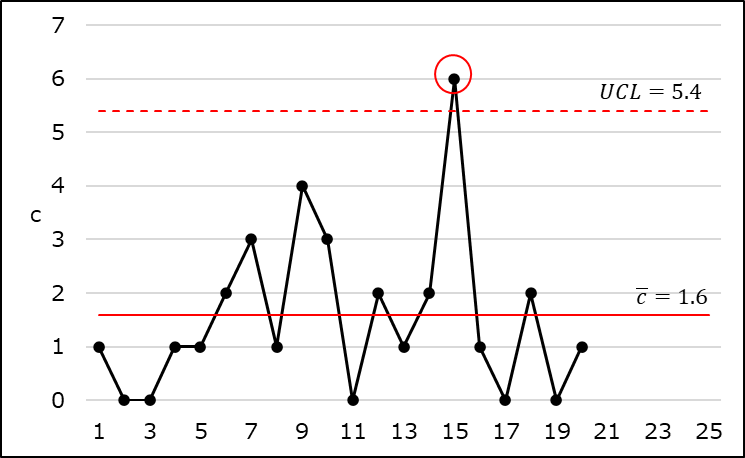
手順4 管理状態の判定
群番号15の打点がUCLを越えていることから、工程は管理状態にあるとは言えないと判定できます。
4. おわりに
今回は、\(c\)管理図の作り方を解説しました。
サンプル自体の合否は問うておらず、あくまでサンプル中の不適合(欠点)の数を管理するのが\(c\)管理図を使う目的であることを意識してください。









