前回、不適合品(不良品)数の管理図である\(np\)管理図の作り方を解説しました。
 工程管理における管理図の活用⑤~np管理図の作り方
工程管理における管理図の活用⑤~np管理図の作り方
\(np\)管理図では群のサンプルの大きさを一定にして、不適合品数を打点しましたが、群のサンプルの大きさを一定にするのが難しい場合があります。
そのようなときに有効な管理図が\(p\)管理図です。
\(p\)管理図は不適合品率(不良率)を打点する管理図で、サンプルの大きさは変わっても構いません。
今回の記事では、\(p\)管理図の作り方を解説します。
1. \(p\)管理図とは
\(p\)管理図は、不適合品率(不良率)\(p\)を使って工程を管理する場合に用いる管理図で、サンプルの大きさは一定である必要はありません。
サンプルの大きさが変わってもよいとなると便利な管理図に感じますが、サンプルの大きさによって管理限界の幅が変わってしまうデメリットがあります。
2. \(p\)管理図の作り方
手順1 データを取る
サンプル中に1~5個程度の不適合品が含まれるような大きさのサンプルを20~25群取り、サンプルを検査して不適合品数を調べます。
手順2 不適合品率\(p\)を計算する
各群の不適合品率\(p\)を計算します。
\(p=\displaystyle \frac{np}{n}\)
ただし、
\(np\):サンプル中の不適合品数
\(n\):1群のサンプルの大きさ
不適合品率をパーセント表示しても、小数点のまま表示しても、どちらでも構いません。
手順3 管理線を計算する
管理線として中心線(CL)、上方管理限界線(UCL)、下方管理限界線(LCL)を計算します。
| \(p\)管理図 | |
|---|---|
| CL | \(\bar{p}=\displaystyle \frac{\sum np}{\sum n}\) \(\sum np\):不適合品数の合計 \(\sum n\):検査個数の合計 |
| UCL | \(\bar{p}+3 \sqrt{\displaystyle \frac {\bar{p}(1-\bar{p})}{n}}\) |
| LCL | \(\bar{p}-3 \sqrt{\displaystyle \frac {\bar{p}(1-\bar{p})}{n}}\) ※値がマイナスになる場合、LCLは考えない。 |
手順4 管理図に記入する
サンプルの不適合品率\(p\)を縦軸に、群の番号を横軸に目盛り、各群の不適合品率を打点します。
さらに、手順3で求めた中心線、UCL、LCLを数値とともに記入します。
通常、中心線は実線、UCLとLCLは破線を用います。
サンプルの大きさが各群で異なる場合は、管理限界線は中心線に対して凸凹になります。
手順5 管理状態にあるかを判定する
3. \(p\)管理図の作成例
20群のデータの例を使って、\(p\)管理図を作成してみましょう。
手順1~2
| No | サンプルサイズ | 不適合品数 | \(p\) |
|---|---|---|---|
| 1 | 888 | 10 | 1.1% |
| 2 | 597 | 8 | 1.3% |
| 3 | 674 | 4 | 0.6% |
| 4 | 198 | 4 | 2.0% |
| 5 | 282 | 7 | 2.5% |
| 6 | 746 | 5 | 0.7% |
| 7 | 307 | 5 | 1.6% |
| 8 | 691 | 12 | 1.7% |
| 9 | 809 | 8 | 1.0% |
| 10 | 222 | 8 | 3.6% |
| 11 | 653 | 6 | 0.9% |
| 12 | 865 | 10 | 1.2% |
| 13 | 695 | 9 | 1.3% |
| 14 | 831 | 12 | 1.4% |
| 15 | 657 | 13 | 2.0% |
| 16 | 816 | 10 | 1.2% |
| 17 | 839 | 13 | 1.5% |
| 18 | 648 | 6 | 0.9% |
| 19 | 705 | 7 | 1.0% |
| 20 | 630 | 4 | 0.6% |
| 合計 | 12753 | 161 |
手順5 管理線の計算
| \(p\)管理図 | |
|---|---|
| CL | \(\bar{p}=\displaystyle \frac{\sum np}{n}=\displaystyle \frac{161}{12753}=1.26%\) |
| UCL | 下表参照 |
| LCL | 下表参照 |
| No | UCL | LCL |
|---|---|---|
| 1 | 2.38% | 0.14% |
| 2 | 2.63% | |
| 3 | 2.55% | |
| 4 | 3.64% | |
| 5 | 3.25% | |
| 6 | 2.49% | 0.03% |
| 7 | 3.17% | |
| 8 | 2.53% | |
| 9 | 2.44% | 0.08% |
| 10 | 3.51% | |
| 11 | 2.57% | |
| 12 | 2.40% | 0.12% |
| 13 | 2.53% | |
| 14 | 2.42% | 0.10% |
| 15 | 2.57% | |
| 16 | 2.43% | 0.09% |
| 17 | 2.42% | 0.10% |
| 18 | 2.57% | |
| 19 | 2.52% | |
| 20 | 2.59% |
※LCLの空白部分は、マイナスの値だったことを示す。
手順4 管理図に記入
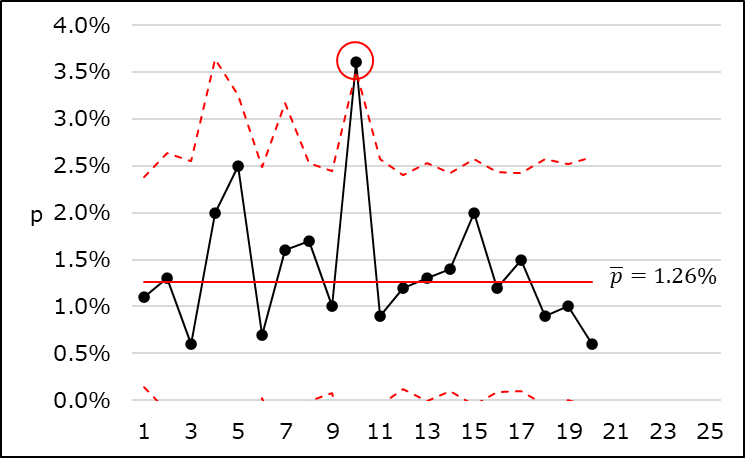
市販の書籍を見ると\(p\)管理図の管理限界線は矩形波で書かれていますが、Excelで矩形波を表示するのは大変なので、一般的な折れ線グラフで表示しています。
手順5 管理状態の判定
群番号10の打点がUCLを越えていることから、工程は管理状態にあるとは言えないと判定できます。
4. おわりに
今回は、\(p\)管理図の作り方を解説しました。
サンプルの大きさが一定でなくてもよいため、\(np\)管理図と違って管理限界がサンプルの大きさによって異なることが大きな特徴です。
管理限界が変わることに抵抗を感じるのであれば、サンプルの大きさを一定にして\(np\)管理図を使いましょう。







