以前の記事で、二つの母平均の差の検定と推定について解説しました。
今回は、データに対応がある場合の母平均の差の検定と推定を解説します。
データの形式が二つの母平均の差のときと同じですが、二つの母平均の差で解説した方法で検定や推定を行うと、誤った判断をする恐れがあります。
「データに対応がある」とはどういうことかをよく考えながら、この記事を読んでいただけましたら幸いです。
 二つの母平均の差に関する検定と推定
二つの母平均の差に関する検定と推定
1. 適用できる場面
以下の事例を使って、データに対応がある場合の母平均の差の検定と推定を解説します。
ある薬品の有効成分量を測定する装置を、更新することになりました。
装置Aと装置Bの測定結果に差があるかどうかを検討するため、過去に生産した製品からランダムに9ロットを選び、装置Aと装置Bで1kg中の有効成分の量を測定したところ、以下のようになりました。(単位:g)
装置Aと装置Bで、測定結果に違いがあると言えるでしょうか。
| ロット | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 装置A | 19.4 | 19.6 | 19.8 | 19.8 | 20.0 | 19.7 | 20.0 | 19.7 | 19.6 |
| 装置B | 19.6 | 19.8 | 19.9 | 20.0 | 20.2 | 19.8 | 19.8 | 20.0 | 19.5 |
2. 対応のあるデータについて
事例1は対応のあるデータの例ですが、対応のあるデータとはどういうことかを詳しく見ていきます。
2-1. 対応のあるデータとは
事例1のデータの形を見ると、二つの母平均の差の検定を使えばよいように見えますが、それだとうまくいきません。
それは、データの性質が異なるためです。
二つの母平均の差の検定では、Aという均一の母集団から\(n_1\)個、Bという均一の母集団から\(n_2\)個のデータが得られることを想定していますが、今回はロットが異なるので、9個のデータが同じ母集団から得られたとは考えられません。
ロット間の変動を考慮して検定と推定を進める必要があります。
今回のデータをグラフにしてみましょう。
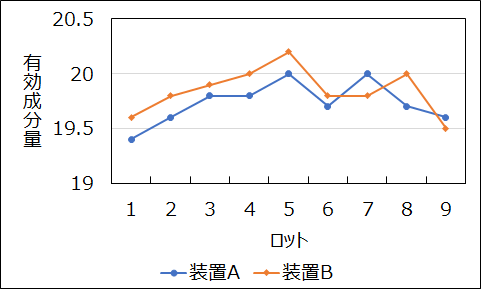
ロット違いによる値の変動は大きく、各ロットにおける装置Aと装置Bの値は、ロット固有の影響を受けていることが分かります。
このように、同一母集団から得られたデータではなく、今回のロットのようにサンプルごとの固有の影響を考慮しなければならないデータを、対応のあるデータと呼びます。
対応のあるデータの例としては、複数の地点から廃水のサンプルを収集し、2つの処理方法AとBでどちらの方法がより多く環境負荷物質を処理できるかなどの事例があります。
廃水中の環境負荷物質の含有量は、地点によって異なるので、これも対応のあるデータに該当します。
2-2. 対応のあるデータを検定するための基本事項
対応のあるデータをもう少し詳しく見てみましょう。
事例1のデータについて、ロット\(i\)の装置Aと装置Bのデータをそれぞれ、\(x_{1i},x_{2i}\)とします。
このとき、\(x_{1i}\)と\(x_{2i}\)の構造は、以下のように表せます。
\(x_{1i}=\mu_1+\gamma_i+\varepsilon_{1i}\)
\(x_{2i}=\mu_2+\gamma_i+\varepsilon_{2i}\)
\(\mu_1\)と\(\mu_2\)が装置Aと装置Bを用いたときの母平均で、今回の解析の目的は、\(\mu_1\)と\(\mu_2\)の母平均について、検定と推定を行うことです。
\(\gamma_i\)はロット\(i\)固有の効果で、\(\gamma_i\)の大小により\(i\)番目のデータ\(x_{1i},x_{2i}\)は同じような傾向で変化します。
\(\varepsilon_{1i}\)と\(\varepsilon_{2i}\)は互いに独立で、それぞれ正規分布\(N(0,\sigma_1^2)\)と\(N(0,\sigma_2^2)\)に従う誤差と考えます。
\(\gamma_i\)は装置Aと装置Bのデータの両方に含まれる共通項なので、\(x_{1i}\)と\(,x_{2i}\)は互いに独立でないため、二つの母平均の差の検定を適用できません。
そこで、対応のあるデータを解析するためには、\(x_{1i}\)と\(x_{2i}\)の差を取って共通項\(\gamma_i\)を消す必要があります。
\(x_{1i}\)と\(x_{2i}\)の差を\(d_i\)とすると、\(d_i\)は以下のように表せます。
\(d_i=x_{1i}-x_{2i}=\mu_1-\mu_2+\varepsilon_{1i}-\varepsilon_{2i}\)
ここで、対応のあるデータを検定するために必要な基本事項をまとめておきます。
対応のあるデータ\(x_{1i},x_{2i}~(i=1,2,\cdots,n)\)があるとき、\(x_{1i}\)と\(x_{2i}\)の差\(d_1,d_2,\cdots,d_n\)は互いに独立で、正規分布\(N(\mu_1-\mu_2,\sigma_d^2)\)に従う。
ただし、\(\sigma_d^2=\sigma_1^2+\sigma_2^2\)である。(分散の加法性)
\(d_1,d_2,\cdots,d_n\)の平均\(\bar{d}\)は、正規分布\(N(\mu_1-\mu_2,\sigma_d^2/n)\)に従う。
\(\bar{d}\)を標準化すると、
\(u=\displaystyle \frac{\bar{d}}{\sqrt{\sigma_d^2/n}} \qquad (1)\)
は標準正規分布\(N(0,1^2)\)に従う。
\(d_1,d_2,\cdots,d_n\)から、平方和\(S_d=\displaystyle \sum_{i=1}^{n}(d_i-\bar{d})^2\)、分散\(V_d=\displaystyle \frac{S_d}{n-1}\)を求め、(1)式の\(\sigma_d^2\)に推定値として\(V_d\)を代入すると、
\(t=\displaystyle \frac{\bar{d}-(\mu_1-\mu_2)}{\sqrt{V_d/n}}\)
は自由度\(\phi=n-1\)の\(t\)分布に従う。
検定では、帰無仮説を\(H_0:\mu_1=\mu_2\)と設定するので、基本事項4から検定統計量\(t_0\)を以下のように設定できます。
\(t_0=\displaystyle \frac{\bar{d}}{\sqrt{V_d/n}}\)
3. データに対応がある場合の母平均の差に関する検定
それでは、データに対応がある場合の母平均の差の検定手順を見ていきます。
基本的な流れは、以前の記事で解説した一つの母平均の検定の流れと同じです。
3-1. データに対応がある場合の母平均の差に関する検定手順
手順1. 帰無仮説\(H_0\)と対立仮説\(H_1\)を設定する。
検定の目的に応じて、(1)~(3)のいずれかを選択します。
(1) \(H_0:\mu_1=\mu_2\)
\(H_1:\mu_1 \neq \mu_2\) (両側検定)
(2) \(H_0:\mu_1=\mu_2\)
\(H_1:\mu_1 > \mu_2\) (右片側検定)
(3) \(H_0:\mu_1=\mu_2\)
\(H_1:\mu_1 < \mu_2\) (左片側検定)
手順2. 有意水準\(\alpha\)を決める。
通常は、\(\alpha=0.05\)とします。
手順3. 手順1(仮説)と手順2(有意水準)に対応した棄却域を決める。
(1)棄却域:\(|t_0|\ge t(\phi,\alpha)\) (両側検定)
(2)棄却域:\(t_0 \ge t(\phi,2\alpha)\) (右片側検定)
(3)棄却域:\(t_0 \le -t(\phi,2\alpha)\) (左片側検定)
手順4. \(n\)組の対応のあるデータ\((x_{1i},x_{2i})~(i=1,2,\cdots,n)\)を取り、検定統計量\(t_0\)を計算する。
\(d_i=x_{1i}-x_{2i}\)
\(\bar{d}=\displaystyle \frac{\sum_{i=1}^{n}d_i}{n}\)
\(S_d=\displaystyle \sum_{i=1}^{n}d_i^2-\displaystyle \frac{\left (\displaystyle \sum_{i=1}^{n}d_i \right )^2}{n}\)
\(V_d=\displaystyle \frac{S_d}{n-1}\)
\(t_0=\displaystyle \frac{\bar{d}}{\sqrt{V_d/n}},~\phi=n-1\)
手順5. 判定する。
\(t_0\)が棄却域に入れば、有意水準\(\alpha\)で有意と判定し、帰無仮説\(H_0\)を棄却して対立仮説\(H_1\)を採択します。
\(t_0\)が棄却域に入らなければ、有意水準\(\alpha\)で有意でないと判定し、帰無仮説\(H_0\)を棄却しません。
3-2. 二つの母平均の差の検定の実施例
事例1について、検定手順に従って検定してみましょう。
実施の前に、予備解析としてあらかじめ\(d_i=x_{1i}-x_{2i}\)を計算しておきます。
| ロット | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 装置A | 19.4 | 19.6 | 19.8 | 19.8 | 20.0 | 19.7 | 20.0 | 19.7 | 19.6 |
| 装置B | 19.6 | 19.8 | 19.9 | 20.0 | 20.2 | 19.8 | 19.8 | 20.0 | 19.5 |
| \(d_i\) | -0.2 | -0.2 | -0.1 | -0.2 | -0.2 | -0.1 | 0.2 | -0.3 | 0.1 |
手順1. 帰無仮説\(H_0\)と対立仮説\(H_1\)を設定する。
装置Aと装置Bで母平均が異なるかどうかを知りたいので、両側検定で帰無仮説と対立仮説を設定します。
\(H_0:\mu_1=\mu_2\)
\(H_1:\mu_1 \neq \mu_2\)
手順2. 有意水準\(\alpha\)を決める。
\(\alpha=0.05\)
手順3. 棄却域を決める。
棄却域:\(|t_0|\ge t(8,0.05)=2.306\)
\((\phi=n-1=9-1=8)\)
手順4. 検定統計量\(t_0\)の値を計算する。
与えられたデータから、
\(\bar{d}=-0.11\)
\(V_d=0.02611\) (Excelの「VAR.S」関数で簡単に求められる)
より、検定統計量\(t_0\)は以下のように求まります。
\(t_0=\displaystyle \frac{\bar{d}}{\sqrt{V_d/n}}=\frac{-0.11}{\sqrt{0.02611/9}}=-2.042\)
手順5. 判定する。
\(t_0=2.042 \lt t(8,0.05)=2.306\)で検定統計量\(t_0\)は採択域に入るので有意ではありません。
よって帰無仮説\(H_0\)を棄却できず、設備Aと設備Bで母平均に差があるとは言えません。
4. データに対応がある場合の母平均の差の推定
母平均の差\(\mu_1-\mu_2\)について、点推定と区間推定ができます。
4-1. データに対応がある場合の母平均の差の推定手順
\(\mu_1-\mu_2\)の点推定は\(\bar(d)\)を使えばよいです。
\(\mu_1-\mu_2\)の区間推定については基本事項4から、
\(Pr \left(-t(\phi,\alpha) <\displaystyle \frac{\bar{d}-(\mu_1-\mu_2)}{\sqrt{V_d/n}}<t(\phi,\alpha)\right)=1-\alpha\)
これを変形すると、以下のようになります。
\(Pr \left ( \bar{d}-t(\phi,\alpha)\sqrt{\displaystyle \frac{V_d}{n}}<\mu_1-\mu_2<\bar{d}+t(\phi,\alpha)\sqrt{\displaystyle \frac{V_d}{n}} \right )\)
\(=1-\alpha \)
左項の括弧内の\(\mu_1-\mu_2\)の範囲が、信頼率\(1-\alpha \)の信頼区間です。
データに対応がある場合の母平均の差の推定手順をまとめると、以下のようになります。
点推定:
\(\hat{\mu_1-\mu_2}=\bar{d}\)
区間推定:信頼率\(1-\alpha\)の信頼区間
\(\left ( \bar{d}-t(\phi,\alpha)\sqrt{\displaystyle \frac{V_d}{n}}, \bar{d}+t(\phi,\alpha)\sqrt{\displaystyle \frac{V_d}{n}} \right )\)
4-2. データに対応がある場合の母平均の差の推定の実施例
事例1について、点推定と区間推定を行ってみましょう。
点推定:
\(\hat{\mu_1-\mu_2}=\bar{d}=-0.11\)
区間推定:信頼率95%の信頼区間を求めます。
\( \left ( \bar{d}-t(8,0.05)\sqrt{\displaystyle \frac{V_d}{n}},\bar{d}+t(8,0.05)\sqrt{\displaystyle \frac{V_d}{n}} \right )\)
\( \left ( -0.11-2.306\sqrt{\displaystyle \frac{0.02611}{9}},-0.11+2.306\sqrt{\displaystyle \frac{0.02611}{9}} \right )\)
\(=(-0.23,0.01)\)
5. 実践のためのアドバイス
二つの母平均の差の検定とデータ形式が同じため、誤使用に気を付ける必要があります。
各データが同一の母集団から得られているとみなせるかどうかをよく確認してから、検定方式を決めることが肝要です。
6. おわりに
今回は、データに対応がある場合の母平均の差に関する検定と推定について解説しました。
データの形式が二つの母平均の差に関する検定と推定に似ていますが、母集団が異なるので、データに対応があるときは検定と推定の進め方に気をつけてください。





