以前の記事で、一つの母分散の検定と推定について基本的な考え方と進め方を解説しました。
基準値となる母分散に対して、着目する母集団の母分散について検定または推定する方法でしたね。
今回は、二つの母集団について両者の母分散が異なるかどうかを検定する方法と母分散の比を推定する方法について解説します。
 一つの母分散に関する検定と推定
一つの母分散に関する検定と推定
1. 適用できる場面
以下の事例を使って、二つの母分散の比の検定と推定を解説します。
ある薬品の1kg中の有効成分の量のばらつきを抑えるため、製造条件を見直すこととしました。
製造条件の変更前後で試作を行い、有効成分の量を測定したところ以下のようになりました。(単位:g)
製造条件の変更前後で、ばらつき(母分散)に違いがあると言えるでしょうか。
変更前:9.87, 9.94, 10.41, 10.06, 9.74, 9.70, 9.87, 9.51, 9.76, 10.32, 9.5, 10.21, 10.05
変更後:10.05, 10.17, 9.86, 9.94, 9.88, 9.93, 10.01, 9.83, 9.9
この事例では、条件変更前の有効成分量の母集団を正規分布\(N(\mu_1,\sigma_1^2)\)、条件変更後の母集団を正規分布\(N(\mu_2,\sigma_2^2)\)と考えて、それぞれの母集団から得られたサンプルのデータに基づいて、二つの母分散\(\sigma_1^2\)と\(\sigma_2^2\)が異なるかどうかの検定と、\(\sigma_1^2\)と\(\sigma_2^2\)の比を推定することが目的です。
なぜ、「比」を考えるのかはこの後で解説します。
2. \(F\)分布について
検定では、帰無仮説\(H_0\)が成り立つことを前提とし、観察事象が確率的に起こり得るかどうかを判断するので、検定統計量が従う分布が必要です。
二つの母分散の比の検定で使える分布が\(F\)分布です。
2-1. F分布とは
第1母集団\(N(\mu_1,\sigma_1^2)\)から得られた\(n_1\)個のサンプル\(x_1,x_2,\cdots,x_{1n_1}\)で、サンプルの分散\(V_1\)と自由度\(\phi_1=n_1-1\)を計算します。
同じように、第2母集団\(N(\mu_2,\sigma_2^2)\)から得られた\(n_2\)個のサンプル\(x_1,x_2,\cdots,x_{2n_2}\)で、サンプルの分散\(V_2\)と自由度\(\phi_2=n_2-1\)を計算します。
このとき、以下の基本事項が成立することが知られています。
\(n_1\)個のデータ\(x_{11},x_{12},\cdots,x_{1n_1}\)が互いに独立に正規分布\(N(\mu_1,\sigma_1^2)\)に従い、また\(n_2\)個のデータ\(x_{21},x_{22},\cdots,x_{2n_2}\)が互いに独立に正規分布\(N(\mu_2,\sigma_2^2)\)に従うとき、\(F=\displaystyle \frac{V_1/\sigma_1^2}{V_2/\sigma_2^2}\)は自由度\((\phi_1=n_1-1,\phi_2=n_2-1)\)の\(F\)分布に従う。
なお、\(\phi_1\)を第1自由度、\(\phi_2\)を第2自由度と言う。
2組の母集団を考えて2つの分散を扱うので、自由度も2つ扱うことになります。
通常、\(F\)の式の分子に対応する自由度を第1自由度とします。
\(F\)分布は2つの自由度によって分布の形状が決まる確率分布です。
また、ゼロ以上の値で定義されていることと、左右非対称の分布形状である点は\(\chi^2\)分布と同じです。
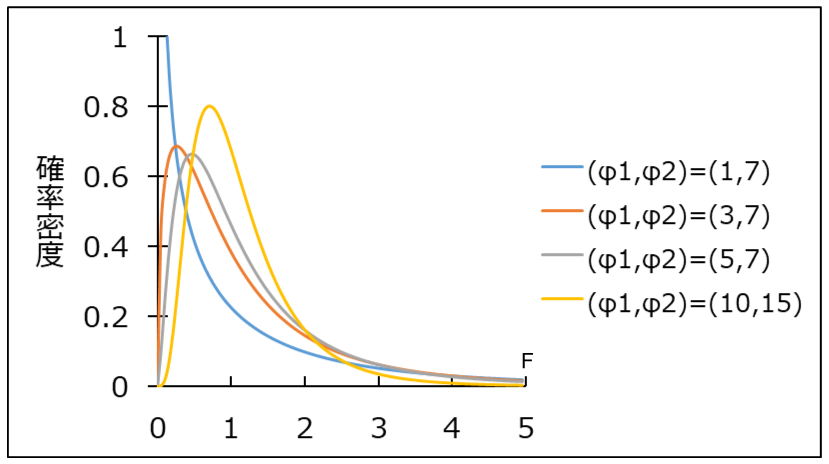
検定統計量が\(F\)分布に従うことが分かれば、あとは棄却域を設定して検定統計量が棄却域に入るかどうかを調べることで検定できます。
2-2. F分布の特徴
自由度\((\phi_1,\phi_2)=(5,10)\)の\(F\)分布を例にとり、\(F\)分布の特徴を解説します。
自由度\((\phi_1,\phi_2)\)の\(F\)分布において、ある点から先の値をとる確率が\(P\)である値は、\(F\)表に与えられています。
この値は、\(F(\phi_1,\phi_2;P)\)と書き、上側\(100P%/)点と言います。(下図における右側の斜線部。\(P=0.05\)の例)

なお、\(F\)分布には下側\(100P%/)点も存在しており、両側検定をしたければ下側\(100P%/)点も必要と思われるかもしれませんが、市販のF表を見ると下側\(100P%/)点は記載されていません。
それは、以下の関係式が成り立つため、上側\(100P%/)点のみで判断できるためです。
\(F(\phi_1,\phi_2;1-P)=\displaystyle \frac{1}{F(\phi_2,\phi_1;P)}~~(1)\)
(1)式において、左辺と右辺で自由度が逆になっていることと、確率が\(1-P\)と\(P\)で異なることに気を付けてください。
(1)式を使うことで、
\(F(5,10;0.95)=\displaystyle \frac{1}{F(10,5;0.05)}=\frac{1}{4.74}=0.21\)
のように、上側\(100P%\)点のみで下側\(100P%\)点をカバーできるのです。
3. 二つの母分散の比に関する検定
それでは、二つの母分散の比の検定手順を見ていきます。
基本的な流れは、以前の記事で解説した一つの母平均および母分散の検定の流れと同じです。
3-1. 二つの母分散の比の検定手順
手順1. 帰無仮説\(H_0\)と対立仮説\(H_1\)を設定する。
検定の目的に応じて、(1)~(3)のいずれかを選択します。
(1) \(H_0:\sigma_1^2=\sigma_2^2\)
\(H_1:\sigma_1^2 \neq \sigma_2^2\) (両側検定)
(2) \(H_0:\sigma_1^2=\sigma_2^2\)
\(H_1:\sigma_1^2 > \sigma_2^2\) (右片側検定)
(3) \(H_0:\sigma_1^2=\sigma_2^2\) (\(\sigma^2_0\)は指定された値)
\(H_1:\sigma_1^2 < \sigma_2^2\) (左片側検定)
手順2. 有意水準\(\alpha\)を決める。
通常は、\(\alpha=0.05\)とします。
手順3. 手順1(仮説)と手順2(有意水準)に対応した棄却域を決める。
(1)棄却域:\(V_1 \ge V_2\)のとき\(F_0=V_1/V_2 \ge F(\phi_1,\phi_2;\,\alpha/2)\)
\(\hspace{4em} V_1 \lt V_2\)のとき\(F_0=V_2/V_1 \ge F(\phi_2,\phi_1;\,\alpha/2)\) (両側検定)
\(\hspace{5em}\) ((1)式を利用)
(2)棄却域:\(F_0=V_1/V_2 \ge F(\phi_1,\phi_2;\,\alpha)\) (右片側検定)
(3)棄却域:(F_0=V_2/V_1 \ge F(\phi_2,\phi_1;\,\alpha)\) (左片側検定)
\(\hspace{5em}\) ((1)式を利用)
手順4. 採取した第1母集団のデータ\(x_{11},x_{12}.\cdots,x_{1n_1}\)と、第2母集団のデータ\(x_{21},x_{22}.\cdots,x_{2n_2}\)から検定統計量\(F_0\)を求める。
\(F_0=\displaystyle \frac{V_1}{V_2}~(V_1 \ge V_2)\) または \(F_0=\displaystyle \frac{V_2}{V_1}~(V_1 \lt V_2)\)
\(\phi_1=n_1-1,~\phi_2=n_2-1\)
手順5. 判定する。
\(F_0\)が棄却域に入れば、有意水準\(\alpha\)で有意と判定し、帰無仮説\(H_0\)を棄却して対立仮説\(H_1\)を採択します。
\(F_0\)が棄却域に入らなければ、有意水準\(\alpha\)で有意でないと判定し、帰無仮説\(H_0\)を棄却しません。
二つの母分散の「比」に関する検定と言うのは、\(V_1\)と\(V_2\)の比を検定統計量にしているためです。
3-2. 二つの母分散の比に関する検定における棄却域の求め方
\(F\)分布は左右非対称のため、両側検定の場合、本来であれば上側と下側の棄却限界値をそれぞれ求める必要があります。
しかし、検定統計量を求めるときに分散の大きい方を分子にすることで、上側のみ棄却限界値を求めればよいのです。
\(F\)分布の棄却限界値をExcelで求める場合、以下のようにセルに入力すれば求められます。(有意水準\(\alpha=0.05\)の場合)
【両側検定】
確率5%を上下に2.5%ずつ割り当てます。
「=F.INV.RT(0.025,\(\phi_1,\phi_2)\))」と入力して得られる値を採用します。
ただし、\(\phi_1\)は検定統計量\(F_0\)の分子にした分散の自由度で、\(F_0\)を求めるときは常に分子に大きい方の分散持ってくるため、検定の際に下側の棄却域を求めることはありません。
【両側検定】
確率5%を上下に2.5%ずつ割り当てます。
「=F.INV.RT(0.025,\(\phi_1,\phi_2)\))」と入力して得られる値を採用します。
ただし、\(\phi_1\)は検定統計量\(F_0\)の分子にした分散の自由度で、\(F_0\)を求めるときは常に分子に大きい方の分散を持ってくるため、検定の際に下側の棄却域を求めることはありません。
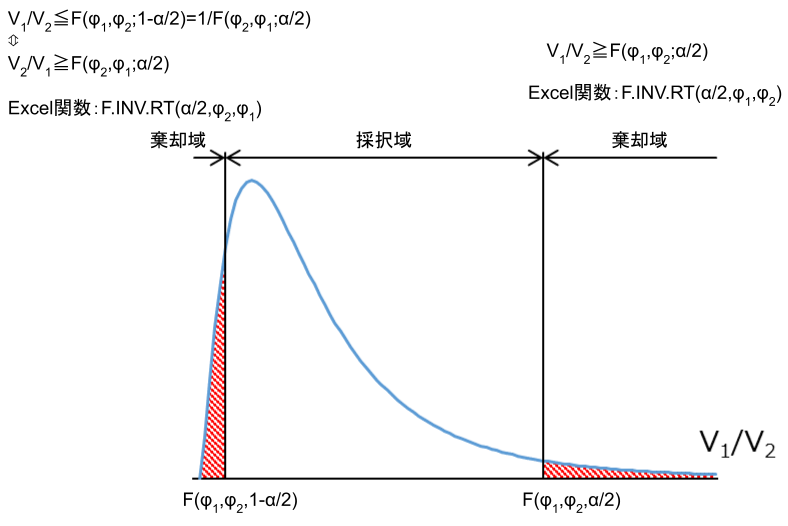
【片側検定】
「=F.INV.RT(0.05,\(\phi_1,\phi_2)\))」と入力して得られる値を採用します。
ただし、\(\phi_1\)は\(F_0\)の分子にした分散の自由度です。
3-3. 二つの母分散の比の検定の実施例
事例1について、検定手順に従って検定してみましょう。
手順1. 帰無仮説\(H_0\)と対立仮説\(H_1\)を設定する。
変更前後で母分散が異なるかどうかを知りたいので、両側検定で帰無仮説と対立仮説を設定します。
\(H_0:\sigma^2_1=\sigma^2_2\)
\(H_1:\sigma^2_1 \neq \sigma^2_2\)
手順2. 有意水準\(\alpha\)を決める。
\(\alpha=0.05\)
手順3. 棄却域を決める。
棄却域:\(V_1 \ge V_2\)のとき、\(F_0=V_1/V_2 \ge F(12,8;0.025)=4.20\)
\(\hspace{3em} V_1 \lt V_2\)のとき、\(F_0=V_2/V_1 \ge F(8,12;0.025)=3.51\)
\(\hspace{3em} (\phi_1=n_1-1=12-1=12,~\phi_2=n_2-1=9-1=8)\)
手順4. 検定統計量\(F_0\)の値を計算する。
得られたデータより、
\(V_1=0.0814\)
\(V_2=0.0112\)
(分散は、Excelの「VAR.S」関数で求められる)
\(V_1 \ge V_2\)なので、\(V_1\)を分子に持ってくる。
\(F_0=\displaystyle \frac{V_1}{V_2}=\frac{0.0814}{0.0112}=7.27\)
手順5. 判定する。
\(F_0=7.27 \ge F(12,8;0.025)=4.20\)で検定統計量\(F_0\)は棄却域に入るので有意です。
よって帰無仮説\(H_0\)を棄却して、製造条件変更前後で母分散は変化したと判断できます。
4. 二つの母分散の比に関する推定
母分散\(\sigma^2\)の比について、点推定と区間推定を実施できます。
ただし、実務では二つの母分散の比を求める機会はあまりないので、他の統計量と同様に推定できることを理解できればよいと思います。
4-1. 二つの母分散の比に関する推定手順
点推定はデータの分散の比\(\displaystyle \frac{V_1}{V_2}\)を使えばよいです。
区間推定については、基本事項から\(F=\displaystyle \frac{V_1/\sigma^2_1}{V_2/\sigma^2_2}\)は自由度\((\phi_1,\phi_2)\)の\(F\)分布に従うことから、以下が成立します。
\(Pr \left(F(\phi_1,\phi_2;1-\alpha/2) <\displaystyle \frac{V_1/\sigma^2_1}{V_2/\sigma^2_2}<F(\phi_1,\phi_2;\alpha/2)\right)=1-\alpha\)
これを変形すると、以下のようになります。
\(Pr \left ( \displaystyle \frac{1}{F(\phi_1,\phi_2;\alpha/2)} \cdot \frac{V_1}{V_2}<\frac{\sigma^2_1}{\sigma^2_2}< \displaystyle \frac{1}{F(\phi_1,\phi_2;1-\alpha/2)} \cdot \frac{V_1}{V_2} \right )\)
\(=1-\alpha \)
左項の括弧内の範囲が、信頼率\(1-\alpha \)の信頼区間です。
二つの母分散に関する比の推定手順をまとめると、以下のようになります。
点推定:
\(\hat{\sigma^2_1/\sigma^2_2}=\displaystyle \frac{V_1}{V_2}\) (Excelの「VAR.S」関数で求められる)
区間推定:信頼率\(1-\alpha\)の信頼区間
\( \left (\displaystyle \frac{1}{F(\phi_1,\phi_2;\alpha/2)} \cdot \frac{V_1}{V_2}, F(\phi_2,\phi_1;\alpha/2) \cdot \frac{V_1}{V_2} \right )\)
4-2. 二つの母分散の比に関する推定の実施例
事例1について、点推定と区間推定を行ってみましょう。
点推定:
\(\hat{\sigma^2_1/\sigma^2_2}=\displaystyle \frac{V_1}{V_2}=\frac{0.0814}{0.0112}=7.27\)
区間推定:信頼率95%の信頼区間を求めます。
\(\left (\displaystyle \frac{1}{F(12,8;0.025)} \cdot \frac{V_1}{V_2}, F(8,12;0.025) \cdot \frac{V_1}{V_2} \right )\)
\( =\left (\displaystyle \frac{1}{4.20} \cdot \frac{0.0814}{0.0112} , 3.51 \cdot \displaystyle \frac{0.0814}{0.0112}\right )\)
\( =(1.73, 25.5)\)
5. 実践のためのアドバイス
母分散の比の検定では、サンプルの分散の大きい方を分子にするというルールがありますが、このルールをうっかり忘れると判断を誤る可能性があるので、注意が必要です。
6. おわりに
今回は、二つの母分散の比に関する検定と推定について解説しました。
棄却限界値を求め方が、これまで解説してきた検定方法と少し求め方が違うので、注意が必要ですが、基本的な考え方と手順は変わりません。
検定統計量を求めるときに、分散の大きい方の値を分子に持ってくることを、しっかり覚えておいてください。





